题目内容
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线A-B-C-D-E表示:从两车出发至快车到达乙地后立即返回到甲地的过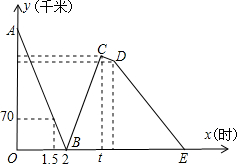 程中y与x之间的函数关系.
程中y与x之间的函数关系.
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t小时,求t的值;
(3)请你直接写出D点的坐标及直线DE的解析式.
 程中y与x之间的函数关系.
程中y与x之间的函数关系.(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t小时,求t的值;
(3)请你直接写出D点的坐标及直线DE的解析式.
分析:(1)把(1.5,70),(2,0)代入一次函数解析式可得线段AB的解析式,让解析式的x等于0可得甲乙两地之间的距离;
(2)设快车的速度为每小时m千米,慢车的速度为每小时n千米,利用辆车行驶距离得出等式方程求出即可;
(3)根据两车行驶方向与速度得出各行驶时间,进而得出D,E点的坐标,即可得出直线DE的解析式.
(2)设快车的速度为每小时m千米,慢车的速度为每小时n千米,利用辆车行驶距离得出等式方程求出即可;
(3)根据两车行驶方向与速度得出各行驶时间,进而得出D,E点的坐标,即可得出直线DE的解析式.
解答:解:(1)设线段AB所在直线的函数关系式为y=kx+b,把(1.5,70)、(2,0)代入得;
,
解得:
∴y=-140x+280;
当x=0时,y=280(2分);
(2)设快车的速度为每小时m千米,慢车的速度为每小时n千米,
由题意得,
,
解得
,
∴t=
=3.5.
(3)根据慢车需要行驶:
=
小时后到达甲地,
此时快车到达乙地后已经行驶:
-3.5=
(小时),
慢车行驶的距离为:
×80=
(km),
故此时两车相距:280-
=
(km),
则D点的坐标为:(
,
),
∵图象是从两车出发至快车到达乙地后立即返回到甲地的过程中y与x之间的函数关系,
∴快车行驶时间为:
×2=7(小时),
则E点坐标为:(7,0),
将(
,
),(7,0),代入一次函数解析式y=ax+c得:
,
解得:
,
直线DE的解析式为:y=-80x+560.
|
解得:
|
∴y=-140x+280;
当x=0时,y=280(2分);
(2)设快车的速度为每小时m千米,慢车的速度为每小时n千米,
由题意得,
|
解得
|
∴t=
| 280 |
| 80 |
(3)根据慢车需要行驶:
| 280 |
| 60 |
| 14 |
| 3 |
此时快车到达乙地后已经行驶:
| 14 |
| 3 |
| 7 |
| 6 |
慢车行驶的距离为:
| 7 |
| 6 |
| 280 |
| 3 |
故此时两车相距:280-
| 280 |
| 3 |
| 560 |
| 3 |
则D点的坐标为:(
| 14 |
| 3 |
| 560 |
| 3 |
∵图象是从两车出发至快车到达乙地后立即返回到甲地的过程中y与x之间的函数关系,
∴快车行驶时间为:
| 280 |
| 80 |
则E点坐标为:(7,0),
将(
| 14 |
| 3 |
| 560 |
| 3 |
|
解得:
|
直线DE的解析式为:y=-80x+560.
点评:此题主要考查了一次函数的应用以及二元一次方程组的应用,根据已知利用图象得出正确信息是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
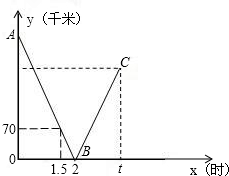 (1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;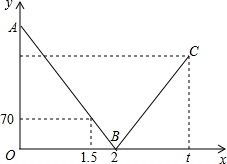 一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图中信息,解答下列问题:
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.根据图中信息,解答下列问题: 至快车到达乙地过程中y与x之间的函数关系.请根据图象进行以下探究:
至快车到达乙地过程中y与x之间的函数关系.请根据图象进行以下探究: