题目内容
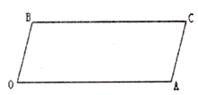
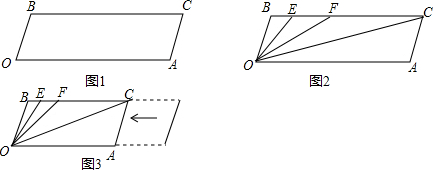
已知, BC∥OA,∠B=∠A=100°,试回答下列问题【小题1】如图1所示,求证:OB‖AC;
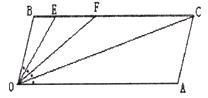
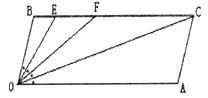
【小题2】如图2,若点E、F在BC上,且满足∠FOC=∠AOC ,并且OE平分∠BOF.试求∠EOC的度数;
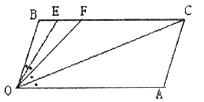
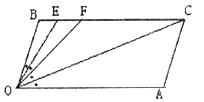
【小题3】在(2)的条件下,若平行移动AC,如图3,则∠OCB:∠OFB的值是 .

【小题1】见解析。
【小题2】400
【小题3】∠OCB:∠OFB=1:2解析:
(1)∵BC∥OA ∴∠B+∠O=1800 ∵∠A=∠B
∴∠A+∠O=1800 ∴OB∥AC
(2)∵∠A=∠B=1000 由(1)得∠BOA=1800-∠B=800
∵ ∠FOC=∠AOC ,并且OE平分∠BOF
∴∠EOF=
 ∠BOF ∠FOC=
∠BOF ∠FOC= ∠FOA
∠FOA ∴∠EOC=∠EOF+∠FOCP=
 (∠BOF+∠FOA)=
(∠BOF+∠FOA)= ∠BOA=400
∠BOA=400 (3) 结论:∠OCB:∠OFB的值不发生变化. 理由为:
∵BC∥OA ∴∠FCO=∠COA
又∵∠FOC=∠AOC ∴∠FOC=∠FCO ∴∠OFB=∠FOC+∠FCO=2∠OCB
∴∠OCB:∠OFB=1:2

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 B=
B=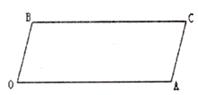
 B=
B=