题目内容
如图，正比例函数y=kx（k＞0），与反比例函数
的图象相交于A，C两点，过A作AB⊥x轴于B，连接BC，若△ABC的面积为S，则
- A.S=1
- B.S=2
- C.S=k
- D.S=k2
A
分析：易得点A与点C关于原点对称，那么所求三角形的面积等于
点A的横坐标的2倍与纵坐标的积．
解答：设点A的坐标为（x，y），则点C的坐标的为（-x，-y）．
∴xy=1
∴S△ABC=×2x×y=xy=1．
故选A．
点评：考查反比例函数k的几何意义的运用；判断出所求三角形的底边为AB，高为A的横坐标的2倍是解决本题的关键．
分析：易得点A与点C关于原点对称，那么所求三角形的面积等于
点A的横坐标的2倍与纵坐标的积．解答：设点A的坐标为（x，y），则点C的坐标的为（-x，-y）．
∴xy=1
∴S△ABC=
×2x×y=xy=1．故选A．
点评：考查反比例函数k的几何意义的运用；判断出所求三角形的底边为AB，高为A的横坐标的2倍是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，正比例函数
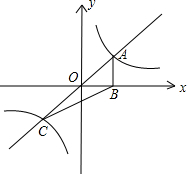如图，正比例函数y=kx（k＞0）与反比例函数y=| 1 |
| x |
| A、S=1 | B、S=2 |
| C、S=3 | D、S的值不能确定 |
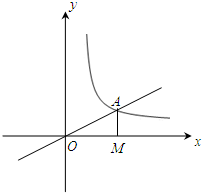如图，正比例函数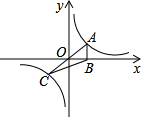y=kx（k＞0）与反比例函数y=
作x轴的垂线，垂足为M，已知△AOM的面积为1，点B（-1，t）为反比例函数在第三象限图象上的点．
已知：如图，正比例函数y=k1x的图象与反比例函数