题目内容
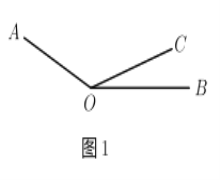
【题目】如图1,![]() ,
,![]() 是线段
是线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() 为边,在
为边,在![]() 的同侧构造菱形
的同侧构造菱形![]() 和菱形
和菱形![]() ,
,![]() 三点在同一条直线上连结
三点在同一条直线上连结![]() ,设射线
,设射线![]() 与射线
与射线![]() 交于
交于![]() .
.
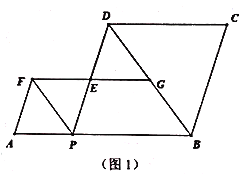
(1)当![]() 在点
在点![]() 的右侧时,求证:四边形
的右侧时,求证:四边形![]() 是平形四边形.
是平形四边形.
(2)连结![]() ,当四边形
,当四边形![]() 恰为矩形时,求
恰为矩形时,求![]() 的长.
的长.
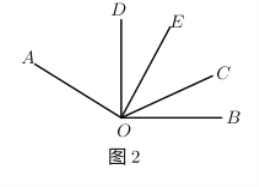
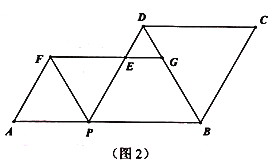
(3)如图2,设![]() ,
,![]() ,记点
,记点![]() 与
与![]() 之间的距离为
之间的距离为![]() ,直接写出
,直接写出![]() 的所有值.
的所有值.
【答案】(1)见解析;(2)FG=![]() ;(3)d=14或
;(3)d=14或![]() .
.
【解析】
(1)由菱形的性质可得AP∥EF,∠APF=∠EPF=![]() ∠APE,PB∥CD,∠CDB=∠PDB=
∠APE,PB∥CD,∠CDB=∠PDB=![]() ∠CDP,由平行线的性质可得∠FPE=∠BDP,可得PF∥BD,即可得结论;
∠CDP,由平行线的性质可得∠FPE=∠BDP,可得PF∥BD,即可得结论;
(2)由矩形的性质和菱形的性质可得FG=PB=2EF=2AP,即可求FG的长;
(3)分两种情况讨论,由勾股定理可求d的值;点G在DP的右侧,连接AC,过点C作CH⊥AB,交AB延长线于点H;若点G在DP的左侧,连接AC,过点C作CH⊥AB,交AB延长线于点H.
(1)∵四边形APEF是菱形
∴AP∥EF,∠APF=∠EPF=![]() ∠APE,
∠APE,
∵四边形PBCD是菱形
∴PB∥CD,∠CDB=∠PDB=![]() ∠CDP
∠CDP
∴∠APE=∠PDC
∴∠FPE=∠BDP
∴PF∥BD,且AP∥EF
∴四边形四边形FGBP是平形四边形;
(2)若四边形DFPG恰为矩形
∴PD=FG,PE=DE,EF=EG,
∴PD=2EF
∵四边形APEF是菱形,四边形PBCD是菱形
∴AP=EF,PB=PD
∴PB=2EF=2AP,且AB=10
∴FG=PB=![]() .
.
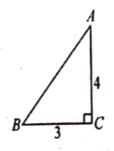
(3)如图,点G在DP的右侧,连接AC,过点C作CH⊥AB,交AB延长线于点H,

∵FE=2EG,
∴PB=FG=3EG,EF=AP=2EG
∵AB=10
∴AP+PB=5EG=10
∴EG=2,
∴AP=4,PB=6=BC,
∵∠ABC=120°,
∴∠CBH=60°,且CH⊥AB
∴BH=![]() BC=3,CH=
BC=3,CH=![]() BH=3
BH=3![]()
∴AH=13
∴AC=![]() =14
=14
若点G在DP的左侧,连接AC,过点C作CH⊥AB,交AB延长线于点H

∵FE=2EG,
∴PB=FG=EG,EF=AP=2EG
∵AB=10,
∴3EG=10
∴EG=![]()
∴BP=BC=![]()
∵∠ABC=120°,
∴∠CBH=60°,且CH⊥AB
∴BH=![]() BC=
BC=![]() ,CH=
,CH=![]() BH=
BH=![]()
∴AH=![]()
∴AC=![]()
综上所述:d=14或![]() .
.