题目内容
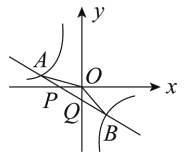
【题目】如图![]() ,已知
,已知![]() ,
,![]() 且
且![]() 、
、![]() 满足等式
满足等式![]() ,射线
,射线![]() 从
从![]() 处绕点
处绕点![]() 以
以![]() 度秒的速度逆时针旋转.
度秒的速度逆时针旋转.
(1)试求∠AOB的度数.
(2)如图![]() ,当射线
,当射线![]() 从
从![]() 处绕点
处绕点![]() 开始逆时针旋转,同时射线
开始逆时针旋转,同时射线![]() 从
从![]() 处以
处以![]() 度/秒的速度绕点
度/秒的速度绕点![]() 顺时针旋转,当他们旋转多少秒时,使得
顺时针旋转,当他们旋转多少秒时,使得![]() ?
?
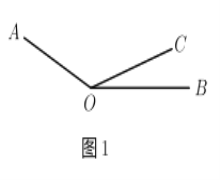
(3)如图![]() ,若射线
,若射线![]() 为
为![]() 的平分线,当射线
的平分线,当射线![]() 从
从![]() 处绕点
处绕点![]() 开始逆时针旋转,同时射线
开始逆时针旋转,同时射线![]() 从射线
从射线![]() 处以
处以![]() 度秒的速度绕点
度秒的速度绕点![]() 顺时针旋转,使得这两条射线重合于射线
顺时针旋转,使得这两条射线重合于射线![]() 处(
处(![]() 在
在![]() 的内部)时,且
的内部)时,且![]() ,试求
,试求![]() .
.
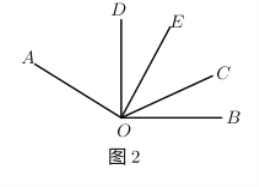
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)根据非负数的性质求得m=140,n=20,即可得到结果;
(2)设他们旋转x秒时,使得∠POQ=10°,则∠AOQ=x°,∠BOP=4x°.分①当射线OP与射线OQ相遇前,②当射线OP与射线OQ相遇后,两种情况,分别列方程求解即可;
(3)设t秒后这两条射线重合于射线OE处,则∠BOE=4t°,先根据角平分线的定义可得∠COD的度数,即可求得∠BOD的度数,再根据![]() 即可求得∠COE的度数,从而得到∠DOE、∠BOE的度数,求出时间t,再列方程求x即可.
即可求得∠COE的度数,从而得到∠DOE、∠BOE的度数,求出时间t,再列方程求x即可.
解:(1)∵![]() ,
,
∴3m420=0且2n40=0,
∴m=140,n=20,
∴∠AOC=140°,∠BOC=20°,
∴∠AOB=∠AOC+∠BOC=160°;
(2)设他们旋转x秒时,使得∠POQ=10°,则∠AOQ=x°,∠BOP=4x°,
①当射线OP与射线OQ相遇前有:∠AOQ+∠BOP+∠POQ=∠AOB=160°,
即:x+4x+10=160,
解得:x=30;
②当射线OP与射线OQ相遇后有:∠AOQ+∠BOP∠POQ=∠AOB=160°,
即:x+4x10=160,
解得:x=34,
答:当他们旋转30秒或34秒时,使得∠POQ=10°;
(3)设t秒后这两条射线重合于射线OE处,则∠BOE=4t°,
∵OD为∠AOC的平分线,
∴∠COD=![]() ∠AOC=70°,
∠AOC=70°,
∴∠BOD=∠COD+∠BOC=70°+20°=90°,
∵![]() ,
,
∴∠COE=![]() ×90°=40°,则∠DOE=70°-40°=30°,∠BOE=20°+40°=60°,
×90°=40°,则∠DOE=70°-40°=30°,∠BOE=20°+40°=60°,
∴4t=60,
解得:t=15,
∴15x=30,
解得:x=2.

 名校课堂系列答案
名校课堂系列答案