题目内容
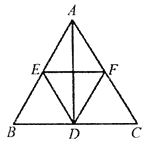
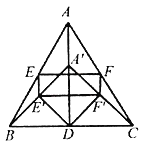
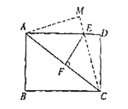
【题目】如图，在正方形ABCD中，点E是 BC边的中点，点B′与点B关于AE对称，BB′与AE交于点F．下列结论错误的是（ ）
A. AB′=AD B. ∠ADB′=75°
C. ∠CB′D=135° D. △FCB′是等腰直角三角形
【答案】B
【解析】分析：根据正方形的性质、对称的性质．全等三角形的性质．四边形内角和等知识，一一判断即可解决问题．
详解：∵四边形ABCD是正方形，∴AB=AD．
∵AB=AB′，∴AB′=AD，故A正确．
∵BF=B′F，BE=CE，∴EF∥CB′．
∵AB=AB′≠BB′，∴∠BAB′≠60，∴∠1≠30°，∴∠2=∠3≠75°，故B错误．
∵∠4=∠5，∠2=∠3．
四边形ABB′D中，易知∠3+∠4=135°，∴∠CB′D=135°，故C正确，
易知△ABF≌BCB′，∴BF=CB′=B′F，故D正确．
故选B．
练习册系列答案
名校课堂系列答案
相关题目
