题目内容
如图，C是线段AB的中点，D是线段BC的中点，已知图中所有的线段之和为39，求线段BC的长．
解：设CD=x，则AC=BC=2x，AD=3x，AB=4x，DB=x．
∴x+2x+2x+3x+4x+x=39
解得x=3
∴BC=2x=6．
答：线段BC的长为6．
分析：结合图形可知，图形中共有6条线段，分别用x的代数式表示出6条线段，根据题意列方程求解即可．
点评：利用中点性质转化线段之间的倍分关系是解题的关键．
∴x+2x+2x+3x+4x+x=39
解得x=3
∴BC=2x=6．
答：线段BC的长为6．
分析：结合图形可知，图形中共有6条线段，分别用x的代数式表示出6条线段，根据题意列方程求解即可．
点评：利用中点性质转化线段之间的倍分关系是解题的关键．
练习册系列答案
相关题目
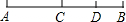如图，C是线段AB的中点，D是CB上一点，下列说法中错误的是（ ）| A、CD=AC-BD | ||
B、CD=
| ||
C、CD=
| ||
| D、CD=AD-BC |
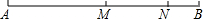
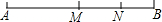如图，M是线段AB的中点，N是线段MB的中点，且NB=6，求AB的长．
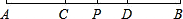如图，P是线段AB的中点，点C、D把线段AB三等份．已知线段CP的长为2cm，求线段AB的长．