题目内容
8.解不等式组$\left\{\begin{array}{l}{x+3>0}\\{2(x-1)+3≥3x}\end{array}\right.$,并判断$\sqrt{2}$是否为该不等式组的解.分析 先分别求出各不等式的解集,再求出其公共解集,判断出$\sqrt{2}$是否在此不等式组解集范围内即可.
解答 解:$\left\{\begin{array}{l}{x+3>0①}\\{2(x-1)+3≥3x②}\end{array}\right.$,
由①得x>-3,
由②得x≤1,
∴原不等式组的解集是-3<x≤1.
∵$\sqrt{2}$>1,
∴$\sqrt{2}$不是该不等式组的解.
点评 本题考查的是解一元一次不等式组及估算无理数的大小,能根据解不等式组的法则求出该不等式组的解集是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.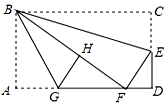 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°; ②AB:DE=AG:DF;
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°; ②AB:DE=AG:DF;