题目内容
如图所示，游戏盘为正六边形，被分成6个面积相等的三角形，每一个三角形都标有相应的数字．甲乙两人投掷飞镖，设甲投掷飞镖所指区域内的数字为x，乙投掷所指区域内的数字为y（当飞镖在边界
线上时，重投一次，直到指向一个区域为止）．
（1）直接写出甲投掷所指区域内的数字为正数的概率；
（2）求出点（x，y）落在第一象限内的概率，并说明理由．
解：（1）P（正数）=
；
（2）根据题意，画表格或画树状图或列举法说明均可
（有列表给4分，若没有列表等不扣分，按照下列标准给分）．
由上图可知，点（x，y）的坐标共有36种等可能的结果，
其中点（x，y）落在第一象限的共有9种，
所以，P（点（x，y）落在第一象限）=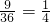
．
分析：因为只有甲乙两人投掷飞镖故甲投掷所指区域内的数字为正数的概率为，点（x，y）落在第一象限内的概率需画图说明．
点评：本题考查学生对简单几何概型的掌握情况，既避免了单纯依靠公式机械计算的做法，又体现了数学知识在现实生活、甚至娱乐中的运用，体现了数学学科的基础性．用到的知识点为：概率=所求情况数与总情况数之比．
；（2）根据题意，画表格或画树状图或列举法说明均可
| 甲 乙 | 1 | 2 | 3 | -1 | -2 | -3 |
| 1 | （1，1） | （2，1） | （3，1） | （-1，1） | （-2，1） | （-3，1） |
| 2 | （1，2） | （2，2） | （3，2） | （-1，2） | （-2，2） | （-3，2） |
| 3 | （1，3） | （2，3） | （3，3） | （-1，3） | （-2，3） | （-3，3） |
| -1 | （1，-1） | （2，-1） | （3，-1） | （-1，-1） | （-2，-1） | （-3，-1） |
| -2 | （1，-2） | （2，-2） | （3，-2） | （-1，-2） | （-2，-2） | （-3，-2） |
| -3 | （1，-3） | （2，-3） | （3，-3） | （-1，-3） | （-2，-3） | （-3，-3） |
由上图可知，点（x，y）的坐标共有36种等可能的结果，
其中点（x，y）落在第一象限的共有9种，
所以，P（点（x，y）落在第一象限）=
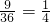．分析：因为只有甲乙两人投掷飞镖故甲投掷所指区域内的数字为正数的概率为
，点（x，y）落在第一象限内的概率需画图说明．点评：本题考查学生对简单几何概型的掌握情况，既避免了单纯依靠公式机械计算的做法，又体现了数学知识在现实生活、甚至娱乐中的运用，体现了数学学科的基础性．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
12、电子跳蚤游戏盘是如图所示的△ABC，AB=6，AC=7，BC=8．如果跳蚤开始时在BC边的P0处，BP0=2．跳蚤第一步从P0跳到AC边的P1（第一次落点）处，且CP1=CP0；第二步从P1跳到AB边的P2（第一次落点）处，且AP2=AP1；第三步从P2跳到BC边的P3（第三次落点）处，且BP3=BP2；…；跳蚤按上述规则一致跳下去，第n次落点为Pn（n为正整数），则点P2007与P2010之间的距离为
线上时，重投一次，直到指向一个区域为止）．
（2012•椒江区二模）电子跳蚤游戏盘是如图所示的△ABC，AB=6，AC=7，BC=8．如果跳蚤开始时在BC边的P0处，BP0=2．跳蚤第一步从P0跳到AC边的P1（第1次落点）处，且CP1=CP0；第二步从P1跳到P2（第2次落点）处，且AP2=AP1；第三步从P2跳到BC边的P3（第3次落点）处，且BP3=BP2；…；跳蚤按上述规则一直跳下去，第n次落点为Pn（n为正整数），则点P2012与P2015之间的距离为（ ）