Question

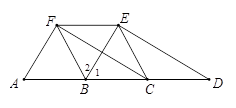
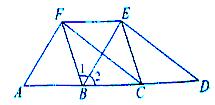
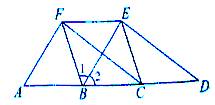
如图，AD∥FE，点B、C在AD上，∠1＝∠2，BF＝BC.

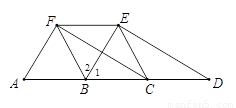
⑴ 求证：四边形BCEF是菱形

⑵ 若AB=BC=CD，求证：△ACF≌△BDE

 

Answer 1

【答案】

⑴⑵见解析，

【解析】⑴根据已知条件证得BCEF是平行四边形，又因为BF＝BC.从而得出结论

⑵证得四边形ABEF、四边形CDEF是平行四边形，即可得出结论

⑴ 证明：∵AD∥FE，

∴∠FEB＝∠1

     又 ∵∠1＝∠2

        ∴∠2＝∠FEB

         ∴BF=EF

∵BF＝BC

∴BC=EF

∴四边形BCEF是平行四边形

∵BF=BC

∴四边形BCEF是菱形

⑵ ∵BC=EF，AB=BC=CD，

∴四边形ABEF、四边形CDEF是平行四边形

∴AF=BE，FC=ED

又 ∵AC=2BC=BD

∴△ACF≌△BDE