题目内容
20.若x+$\frac{1}{x}$=2,求(1)x2+$\frac{1}{{x}^{2}}$的值.
(2)x4+$\frac{1}{{x}^{4}}$
(3)x-$\frac{1}{x}$.
分析 根据完全平方公式得出(x+$\frac{1}{x}$)2=4,展开从而得出x2+$\frac{1}{{x}^{2}}$的值;再对x2+$\frac{1}{{x}^{2}}$两边平方即可得出x4+$\frac{1}{{x}^{4}}$的值;根据(x+$\frac{1}{x}$)2=(x-$\frac{1}{x}$)2+4,从而得出x-$\frac{1}{x}$的值.
解答 解:(1)∵x+$\frac{1}{x}$=2,
∴(x+$\frac{1}{x}$)2=4,
∴x2+$\frac{1}{{x}^{2}}$=2;
(2)∵x2+$\frac{1}{{x}^{2}}$=2,
∴(x2+$\frac{1}{{x}^{2}}$)2=4,
∴x4+$\frac{1}{{x}^{4}}$=2;
(3)∵(x+$\frac{1}{x}$)2=(x-$\frac{1}{x}$)2+4,
∴x-$\frac{1}{x}$=0.
点评 本题考查了分式的混合运算,掌握完全平方的变形是解题的关键.

练习册系列答案
相关题目
11.在直角坐标系中有点A(O,3)、B(-5,-3)、C(6,-2),那么△ABC是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
8.如果9xm-5-y3n+2=10是二元一次方程,那么( )
| A. | m=6,n=-$\frac{1}{3}$ | B. | m=-6,n=$\frac{1}{3}$ | C. | m=5,n=-$\frac{2}{3}$ | D. | m=-5,n=$\frac{2}{3}$ |
12.若有理数m,n,满足m-2n=4,2m-n=3,则m+n等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
9.下列函数:①y=2x;②y=3+4x;③y=$\frac{1}{2}$;④y=ax(a≠0的常数);⑤xy=3;⑥$\frac{x}{y}$=5.其中是正比例函数的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
15.使|-2015+( )|=|-2015|+|( )|成立,括号内应填的数是( )
| A. | 任意一个正有理数 | B. | 任意一个大于-2015的数 | ||
| C. | 任意一个负数 | D. | 任意一个非正数 |
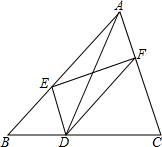 如图,D为△ABC边BC上的一点,DE∥AC,DF∥AB,连接AD,EF.求证:AD,EF互相平分.
如图,D为△ABC边BC上的一点,DE∥AC,DF∥AB,连接AD,EF.求证:AD,EF互相平分.