题目内容
如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求DE的长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长 .

解:(1)由题意可知,抛物线的对称轴为:x=6
∴设抛物线的解析式为
 ∵抛物线经过点A(3,0)和C(0,9)
∵抛物线经过点A(3,0)和C(0,9)
∴
解得:
∴ 
(2)连接AE
∵DE是⊙A的切线,∴∠AED=90°,AE=3
∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点
∴AB=BD=3
∴AD=6
在Rt△ADE中,
∴
(3)当BF⊥ED时
∵∠AED=∠BFD=90°
∠ADE=∠BDF
∴△AED∽△BFD
∴
即
∴

当FB⊥AD时
∵∠AED=∠FBD=90°
∠ADE=∠FDB
∴△AED∽△FBD
∴
即
∴当△BFD与EAD△相似时,BF的长为 或
或

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. (2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.
(2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.
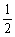 S△ACD D.DE平分∠CDF
S△ACD D.DE平分∠CDF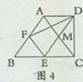
 (k≠0)的图像过等边三角形AOB的顶点A,已知点B(-2,0)。(1)求反比例函数的表达式;
(k≠0)的图像过等边三角形AOB的顶点A,已知点B(-2,0)。(1)求反比例函数的表达式;
 B.
B.
 D.
D.
 、0.2、
、0.2、 、
、
 、
、 、
、 中,无理数的个数是__________.
中,无理数的个数是__________.