题目内容
 如图,半圆的直径AB=10.弦AC=6,把AC沿直线AD对折恰与AB重合,点C落在C′处,则AD的长为( )
如图,半圆的直径AB=10.弦AC=6,把AC沿直线AD对折恰与AB重合,点C落在C′处,则AD的长为( )分析:设圆的圆心是O,连接OD,作DE⊥AB于E,OF⊥AC于F,运用圆周角定理,可证得∠DOB=∠OAC,即证△AOF≌△OED,所以OE=AF=3,根据勾股定理,得DE=4,在直角三角形ADE中,根据勾股定理,可求AD的长.
解答: 解:设圆的圆心是O,连接OD,作DE⊥AB于E,OF⊥AC于F.
解:设圆的圆心是O,连接OD,作DE⊥AB于E,OF⊥AC于F.
根据题意知,∵OF⊥AC,
∴AF=
AC=3,
∵∠CAD=∠BAD,
∴
=
,
∴点D是弧BC的中点.
∴∠DOB=∠OAC=2∠BAD,
在△AOF和△OED中,
,
∴△AOF≌△OED(AAS),
∴OE=AF=3,
∵DO=5,
∴DE=4,
∴AD=
=
=
=4
.
故选A.
 解:设圆的圆心是O,连接OD,作DE⊥AB于E,OF⊥AC于F.
解:设圆的圆心是O,连接OD,作DE⊥AB于E,OF⊥AC于F.根据题意知,∵OF⊥AC,
∴AF=
| 1 |
| 2 |
∵∠CAD=∠BAD,
∴
 |
| CD |
 |
| BD |
∴点D是弧BC的中点.
∴∠DOB=∠OAC=2∠BAD,
在△AOF和△OED中,
|
∴△AOF≌△OED(AAS),
∴OE=AF=3,
∵DO=5,
∴DE=4,
∴AD=
| DE2+AE2 |
| 42+82 |
| 80 |
| 5 |
故选A.
点评:此题主要考查了翻折变换的性质以及垂径定理、圆周角定理和勾股定理等知识,在圆的有关计算中,作弦的弦心距是常见的辅助线之一.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
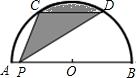 如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,则阴影部分的面积等于
如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,则阴影部分的面积等于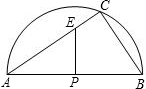 如图,半圆的直径AB=10,P为圆心,点C在半圆上,BC=6.
如图,半圆的直径AB=10,P为圆心,点C在半圆上,BC=6. (1997•新疆)如图,半圆的直径AB=3,点C在半圆上,点E在AC上,且AE=BC,EF⊥AB于点F.若设BC=x,EF=y,则y关于x的函数关系式为y=
(1997•新疆)如图,半圆的直径AB=3,点C在半圆上,点E在AC上,且AE=BC,EF⊥AB于点F.若设BC=x,EF=y,则y关于x的函数关系式为y= 如图,半圆的直径AB=10,点C在半圆上,BC=6.
如图,半圆的直径AB=10,点C在半圆上,BC=6.