ЬтФПФкШн
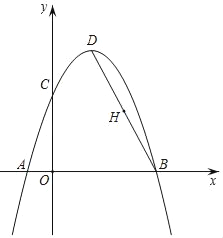
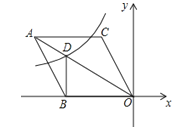
ЁОЬтФПЁПШчЭМ1ЃЌФГаЃгавЛПщСтаЮПеЕиABCDЃЌЁЯA=60ЁуЃЌAB=40mЃЌЯжМЦЛЎдкФкВПаоНЈвЛИіЫФИіЖЅЕуЗжБ№ТфдкСтаЮЫФЬѕБпЩЯЕФОиаЮгуГиEFGHЃЌЦфгрВПЗжжжЛЈВнЃЌдАСжЙЋЫОаоНЈгуГиЃЌВнЦКЕФдьМлЮЊyЃЈдЊЃЉгыаоНЈУцЛ§sЃЈm2ЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМ2ЫљЪОЃЌЩшAEЮЊxУзЃЎ
ЃЈ1ЃЉЬюПеЃКED=ЁЁ ЁЁmЃЌEH=ЁЁ ЁЁmЃЌЃЈгУКЌxЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈЬсЪОЃКдкжБНЧШ§НЧаЮжаЃЌ30ЁуНЧЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЃЉ
ЃЈ2ЃЉШєОиаЮгуГиEFGHЕФУцЛ§ЪЧ300![]() m2ЃЌЧѓEFЕФГЄЖШЃЛ
m2ЃЌЧѓEFЕФГЄЖШЃЛ
ЃЈ3ЃЉEFЕФГЄЖШЮЊЖрЩйЪБЃЌаоНЈЕФгуГиКЭВнЦКЕФзмдьМлзюЕЭЃЌзюЕЭдьМлЮЊЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ
ЃЛ![]() ЃЛ ЃЈ2ЃЉ10mЛђ30mЃЛЃЈ3ЃЉx=20ЪБЃЌзмдьМлзюаЁЃЌзюаЁжЕЮЊ
ЃЛ ЃЈ2ЃЉ10mЛђ30mЃЛЃЈ3ЃЉx=20ЪБЃЌзмдьМлзюаЁЃЌзюаЁжЕЮЊ![]() дЊЃЛ
дЊЃЛ
ЁОНтЮіЁП
(1)жБНгаДГіНсЙћМДПЩ.
(2)СЌНгDBЃЌХаЖЈЁїAEFЮЊЕШБпШ§НЧаЮЃЌДгЖјEF=xЃЌРћгУ(1)жаEHЕФГЄЃЌИљОнОиаЮУцЛ§ЙЋЪНСаГіЗНГЬЃЌНтГіxМДПЩ.
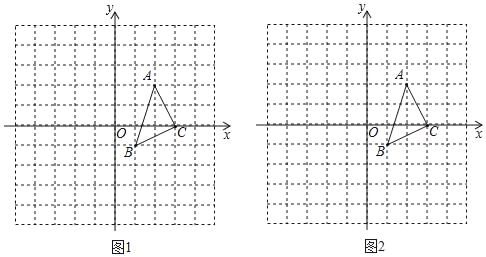
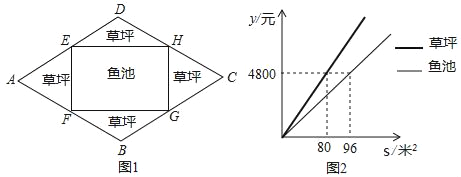
(3)ИљОнЭМ2ЕУГіВнЦККЭгуГиЕФМлЃЌЗжБ№ЧѓГіВнЦККЭгуГиЕФУцЛ§(гУКЌxЕФЪНзгБэЪО)ЃЌДгЖјЕУЕНвЛИізмМлЮЊвЛИіЙигкxЖўДЮКЏЪ§ЃЌНЋЦфаДГЩЖЅЕуЪНЃЌБуПЩЕУГіКЏЪ§ЕФзюжЕ.
ЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСЌНг![]() ЃЌдђEFЁЮDB
ЃЌдђEFЁЮDB
Ёр![]()
Ёп ![]()
Ёр![]()
гж![]()
ЁрЁї![]() ЪЧЕШБпШ§НЧаЮ
ЪЧЕШБпШ§НЧаЮ
Ёр![]()
гЩЃЈ1ЃЉПЩжЊ![]()
Ёр![]()
![]()
![]()
НтЕУ![]() ЃЌ
ЃЌ![]() ОМьбщОљЗћКЯЬтвтЃЌ
ОМьбщОљЗћКЯЬтвтЃЌ
Д№ЃК![]() ЕФГЄЖШ10
ЕФГЄЖШ10![]() Лђ30
Лђ30![]() ЁЃ
ЁЃ
ЃЈ3ЃЉвРЬтвтЕУВнЦКЕЅМлЮЊЃК4800ЁТ80=60дЊ/Уз2ЃЌ
гуГиЕЅМлЮЊЃК4800ЁТ96=50дЊ/Уз2ЃЌ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌЁЯBAD=60ЁуЃЌAB=40mЃЌЁрBD=40ЃЌAC=![]() ЃЌ
ЃЌ
ЁрСтаЮABCDЕФУцЛ§ЪЧЃК![]()
![]() ЃЌ
ЃЌ
ЁпОиаЮEFGHЕФУцЛ§ЪЧЃК![]()
ЁрВнЦКЕФУцЛ§ЪЧЃК![]()
змдьМлЮЊЃК![]()
![]()
![]()
Ёп![]()
ЁрЕБ![]() ЪБЃЌзмдьМлзюаЁЃЌзюаЁжЕЮЊ
ЪБЃЌзмдьМлзюаЁЃЌзюаЁжЕЮЊ![]() дЊ
дЊ
Д№ЃКEFЕФГЄЖШЮЊ20mЪБЃЌаоНЈЕФгуГиКЭВнЦКЕФзмдьМлзюЕЭЃЌзюЕЭдьМл![]() дЊЃЎ
дЊЃЎ
ЙЪД№АИЮЊЃКЃЈ1ЃЉ![]() ЃЛ
ЃЛ![]() ЃЛ ЃЈ2ЃЉ10mЛђ30mЃЛЃЈ3ЃЉx=20ЪБЃЌзмдьМлзюаЁЃЌзюаЁжЕЮЊ
ЃЛ ЃЈ2ЃЉ10mЛђ30mЃЛЃЈ3ЃЉx=20ЪБЃЌзмдьМлзюаЁЃЌзюаЁжЕЮЊ![]() дЊ.
дЊ.

 ССЕуМЄЛюОЋБрЬсгХ100ЗжДѓЪдОэЯЕСаД№АИ
ССЕуМЄЛюОЋБрЬсгХ100ЗжДѓЪдОэЯЕСаД№АИ