题目内容
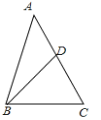
【题目】已知：如图，AB=AC，AE=AF，连结BF，CE，交于O，连结AO．求证：
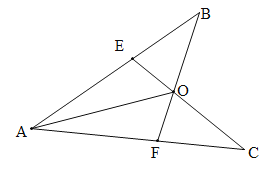
（1）∠B=∠C
（2）AO平分∠BAC
【答案】（1）答案见解析；（2）答案见解析
【解析】
（1）由SAS证得△AEC≌△AFB，即可得出结论；
（2）先证△EBO≌△FCO，得出OB=OC，再由SSS证明△AOB≌△AOC，即可得出结论．
（1）在△AEC与△AFB中，∵AE=AF，∠EAF=∠EAF，AC=AB，∴△AEC≌△AFB（SAS），∴∠C=∠B；
（2）∵AB=AC，AE=AF，∴BE=CF．
在△BEO和△CFO中，∵∠B=∠C，∠EOB=∠FOC，BE=CF，∴△BEO≌△CFO，∴BO=CO．
在△AOB和△AOC中，∵AB=AC，AO=AO，OB=OC，∴△AOB≌△AOC，∴∠BAO=∠CAO，∴AO平分∠BAC．
练习册系列答案
相关题目
【题目】为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收贵的价目表如下(注：水费按月份结算，
表示立方米)
价目表 | |
每月用水量 | 价格 |
不超过 |
|
超出 |
|
超出 |
|
某户居民1月份和2月份的用水量分别为
和
，则应收水费分别是 元和 元
若该户居民
月份用水量
(其中
)，则应收水费多少元? (用含
的式子表示，并化简)
若该户居民
两个月共用水 
(
月份用水量超过
月份)，设月份用水
，求该户居民两个月共交水费多少元? (用含 
的式子表示，并化简)
