Question

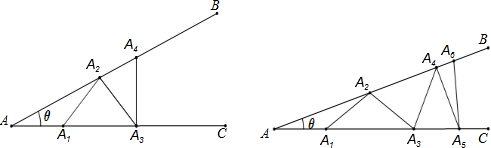
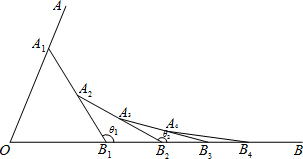
如图，已知∠AOB=α，在射线OA、OB上分别取点OA₁=OB₁，连接A₁B₁，在B₁A₁、B₁B上分别取点A₂、B₂，使B₁B₂=B₁A₂，连接A₂B₂…按此规律上去，记∠A₂B₁B₂=θ₁，∠A₃B₂B₃=θ₂，…，∠A_n+1B_nB_n+1=θ_n，则θ₂₀₁₂-θ₂₀₁₁的值为（　　）

A． 180°-α 22012	B． 180°+α 22012
C． 180°-α 22011	D． 180°+α 22011

Answer 1

∵OA₁=OB₁，∠AOB=α，
∴∠A₁B₁O=

1

2

（180°-α），
∴

1

2

（180°-α）+θ₁=180，
整理得，θ₁=

180°+α

2

，
∵B₁B₂=B₁A₂，∠A₂B₁B₂=θ₁，
∴∠A₂B₂B₁=

1

2

（180°-θ₁），
∴

1

2

（180°-θ₁）+θ₂=180°，
整理得，θ₂=

180°+θ1

2

=

3×180°+α

4

，
∴θ₂-θ₁=

3×180°+α

4

-

180°+α

2

=

180°-α

4

=

180°-α

22

，
同理可求θ₃=

180°+θ2

2

=

7×180°+α

8

，
∴θ₃-θ₂=

7×180°+α

8

-

3×180°+α

4

=

180°-α

8

=

180°-α

23

，
…，
依此类推，θ₂₀₁₂-θ₂₀₁₁=

180°-α

22012

．
故选A．