题目内容
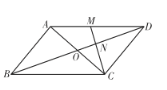
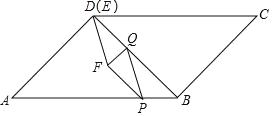
【题目】如图,BD是ABCD的对角线,AD⊥BD,AB=2![]() cm,∠A=45°.动点P从点B出发,以
cm,∠A=45°.动点P从点B出发,以![]() cm/s的速度沿BA运动到终点A,同时动点Q从点D出发,以2cm/s的速度沿折线DB﹣BC向终点C运动,当一点到达终点时另一点也停止运动.过点Q作QE⊥AD,交射线AD于点E,连接PQ,以PQ与EQ为边作PQEF.设点P的运动时间为t(s),PQEF与ABCD重叠部分图形的面积为S(cm2).
cm/s的速度沿BA运动到终点A,同时动点Q从点D出发,以2cm/s的速度沿折线DB﹣BC向终点C运动,当一点到达终点时另一点也停止运动.过点Q作QE⊥AD,交射线AD于点E,连接PQ,以PQ与EQ为边作PQEF.设点P的运动时间为t(s),PQEF与ABCD重叠部分图形的面积为S(cm2).
(1)AP= cm(用含的代数式表示);
(2)当点F落在边AD上时,求t的值:
(3)求S与t之间的函数关系式;
(4)连接FQ,当FQ所在的直线将ABCD分成面积相等的两部分时,直接写出t的值.
【答案】(1)2![]() ﹣
﹣![]() t(2)
t(2)![]() (3)S=
(3)S=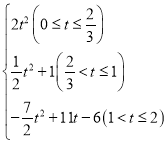 (4)t=
(4)t=![]() 或t=
或t=![]()
【解析】
(1)先根据点P的运动速度和时间可得PB的长,从而得AP的长;
(2)根据BQ=PQ=BDDQ,列方程可得结论;也可以根据平行四边形的性质可得PF=QE,据此列出方程求出t的值即可;
(3)分三种情况分别求出S与t的函数关系式即可:①当0<t≤![]() 时,
时,![]() PQEF与
PQEF与![]() ABCD重叠部分为矩形;②当
ABCD重叠部分为矩形;②当![]() <t≤1时,
<t≤1时,![]() PQEF与
PQEF与![]() ABCD重叠部分为梯形;③当1<t≤2时,
ABCD重叠部分为梯形;③当1<t≤2时,![]() PQEF与
PQEF与![]() ABCD重叠部分为五边形.
ABCD重叠部分为五边形.
(4)当直线FQ将![]() ABCD分成面积相等的两部分时,则Q必在对角线BD中点或直线FQ经过对角线BD中点,据此解答即可.
ABCD分成面积相等的两部分时,则Q必在对角线BD中点或直线FQ经过对角线BD中点,据此解答即可.
解:(1)由题意得:PB=![]() t,
t,
∵AB=2![]() ,
,
∴AP=AB﹣PB=2![]() ﹣
﹣![]() t;
t;
故答案为(2![]() ﹣
﹣![]() t);
t);
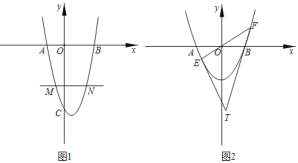
(2)如图1,当点F落在边AD上,
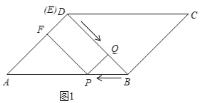
由题意得:DQ=2t,PB=![]() t,
t,
∵四边形PQEF是平行四边形,
∴PQ∥EF,
∴∠BPQ=∠A=45°,∠BQP=∠ADB=90°,
∴PQ=BQ=t,
∵△ADB是等腰直角三角形,且AB=2![]() ,
,
∴BD=2,
∴BQ=BD﹣DQ=2﹣2t,
即t=2﹣2t,
∴t=![]() ,
,
则当点F落在边AD上时,t的值![]() 秒;
秒;
(3)分两种情况:
①当0<t≤![]() 时,Q在BD上,如图1,过P作PM⊥BD于M,则△BPM是等腰直角三角形,
时,Q在BD上,如图1,过P作PM⊥BD于M,则△BPM是等腰直角三角形,

∵PB=![]() t,
t,
∴PM=t,
∴S=DQPM=2tt=2t2;
②当![]() <t≤1时,Q在BD上,如图3,过Q作QH⊥AB于H,
<t≤1时,Q在BD上,如图3,过Q作QH⊥AB于H,
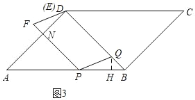
∵BQ=2﹣2t,
∴QH=![]() (2﹣2t),
(2﹣2t),
∵PF∥BD,∠ADB=90°,
∴∠ANP=90°,
∵AP=2![]() ﹣
﹣![]() t,
t,
∴AN=PN=2﹣t,
∴S=S△ADB﹣S△ANP﹣S△PBQ=![]() ﹣
﹣![]() =
=![]() t2+t.
t2+t.
③当1<t≤2时,如图4,Q在BC上,
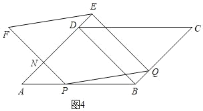
同②知:AN=PN=2﹣t,
∵EQ∥BD,DE∥BQ,
∴四边形BDEQ是平行四边形,∠DEQ=90°,
∴EQ=span>BD=2,BQ=DE=2t﹣2,
∵EN=DN+DE=2﹣(2﹣t)+(2t﹣2)=3t﹣2,
S=![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() =﹣
=﹣![]() t2+11t﹣6;
t2+11t﹣6;
综上,S与t之间的函数关系式为:S=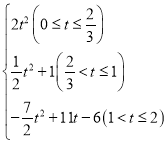 ;
;
(4)存在两种情况:
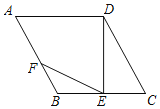
①当FQ过BD的中点O时,如图5,则OB=OD=1,
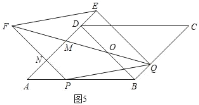
∵∠DOM=∠BOQ,∠MDO=∠OBQ,
∴△MDO≌△QBO(ASA),
∴BQ=DM=DE=2t﹣2,
∴MN=EN﹣2DM=(3t﹣2)﹣2(2t﹣2)=2﹣t,
∵AN=PN=2﹣t,
∴FN=t,
∵∠NFM=∠BOQ,
∴tan∠NFM=tan∠BOQ,即![]() ,
,
∴![]() ,
,
2t2﹣t﹣2=0,
t=![]() 或
或![]() ;
;
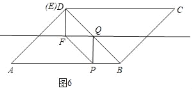
②当Q在BD的中点上时,如图6,则2t=1,t=![]() ;
;
综上,t=![]() 秒或t=
秒或t=![]() 秒.
秒.

 发散思维新课堂系列答案
发散思维新课堂系列答案