题目内容
(11·孝感)如图,直线AB、CD交于点O,OT⊥AB于O,CE∥AB交CD于
点C,若∠ECO=30°,则∠DOT等于( )
A. 30° B. 45° C. 60° D. 120°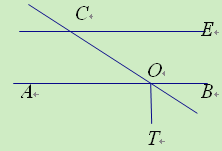
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
题目内容
(11·孝感)如图,直线AB、CD交于点O,OT⊥AB于O,CE∥AB交CD于
点C,若∠ECO=30°,则∠DOT等于( )
A. 30° B. 45° C. 60° D. 120°
 备战中考寒假系列答案
备战中考寒假系列答案