题目内容
某年级利用暑假组织学生外出旅游,有10名家长代表随团出行,甲旅行社说:“如果10名家长代表都买全票,则其余学生可享受半价优惠”;乙旅行社说:“包括10名家长代表在内,全部按票价的6折(即按全标的60%收费)优惠”,若全票价为40元,
(1)如果学生人数为30人,旅行社收费多少元?如果学生人数为70人,旅行社收费多少元?
(2)当学生人数为多少时,两家旅行社的收费一样?
(3)选择哪个旅行社更省钱?
解:(1)甲旅行社收费:10×40+30×40×50%=1000(元);
乙旅行社收费:(10+30)×40×60%=960(元);
甲旅行社收费:10×40+70×40×50%=1800(元);
乙旅行社收费:(10+70)×40×60%=1920(元);
(2)设学生人数为x时,两家旅行社的收费一样,由题意得:
10×40+40x×50%=(10+x)×40×60%,
解得:x=40,
答:学生人数为40时,两家旅行社的收费一样;
(3)设学生人数为x时,
甲旅行社的收费是:10×40+40×50%•x,
乙旅行社的收费是:(10+x)×40×60%,
①当选择甲旅行社更省钱时:10×40+40×50%•x<(10+x)×40×60%,
解得:x>40,
②当选择乙旅行社更省钱时:10×40+40×50%•x>(10+x)×40×60%,
解得:x<40,
③当选择两个旅行社花钱一样多时:10×40+40×50%•x=(10+x)×40×60%,
解得:x=40,
答:当学生少于40人时,选择乙更便宜,当学生多于40人时,选择甲便宜,当学生等于40人时,选哪个都一样.
分析:(1)根据题意可知:甲旅行社收费=10名家长代表×40+学生数×40×50%;乙旅行社收费=(10名家长代表+学生数)×40×60%,代入学生数即可求出收费;
(2)设学生人数为x时,两家旅行社的收费一样,根据题意可得等量关系:10名家长代表×40+学生数×40×50%=(10名家长代表+学生数)×40×60%,由等量关系可得方程:10×40+40x×50%=(10+x)×40×60%,解方程可得答案;
(3)设学生人数为x,分别表示出甲旅行社的收费:10×40+40×50%•x,乙旅行社的收费是:(10+x)×40×60%,根据省钱情况可列出不等式,再解不等式即可.
点评:此题主要考查了一元一次方程,一元一次不等式的应用,正确理解甲、乙两个旅行社的收费标准;找到相应的等量关系和不等关系是解决问题的关键.
乙旅行社收费:(10+30)×40×60%=960(元);
甲旅行社收费:10×40+70×40×50%=1800(元);
乙旅行社收费:(10+70)×40×60%=1920(元);
(2)设学生人数为x时,两家旅行社的收费一样,由题意得:
10×40+40x×50%=(10+x)×40×60%,
解得:x=40,
答:学生人数为40时,两家旅行社的收费一样;
(3)设学生人数为x时,
甲旅行社的收费是:10×40+40×50%•x,
乙旅行社的收费是:(10+x)×40×60%,
①当选择甲旅行社更省钱时:10×40+40×50%•x<(10+x)×40×60%,
解得:x>40,
②当选择乙旅行社更省钱时:10×40+40×50%•x>(10+x)×40×60%,
解得:x<40,
③当选择两个旅行社花钱一样多时:10×40+40×50%•x=(10+x)×40×60%,
解得:x=40,
答:当学生少于40人时,选择乙更便宜,当学生多于40人时,选择甲便宜,当学生等于40人时,选哪个都一样.
分析:(1)根据题意可知:甲旅行社收费=10名家长代表×40+学生数×40×50%;乙旅行社收费=(10名家长代表+学生数)×40×60%,代入学生数即可求出收费;
(2)设学生人数为x时,两家旅行社的收费一样,根据题意可得等量关系:10名家长代表×40+学生数×40×50%=(10名家长代表+学生数)×40×60%,由等量关系可得方程:10×40+40x×50%=(10+x)×40×60%,解方程可得答案;
(3)设学生人数为x,分别表示出甲旅行社的收费:10×40+40×50%•x,乙旅行社的收费是:(10+x)×40×60%,根据省钱情况可列出不等式,再解不等式即可.
点评:此题主要考查了一元一次方程,一元一次不等式的应用,正确理解甲、乙两个旅行社的收费标准;找到相应的等量关系和不等关系是解决问题的关键.

练习册系列答案
相关题目
 某制笔企业欲将200件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地.
某制笔企业欲将200件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地.
(1)根据信息填表:
| A地 | B地 | C地 | 合计 | |
| 产品件数(件) | x | 2x | 200 | |
| 运费(元) | 30•x |
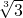



 ________
________ .
. 如图是由三个小方体叠成的一个立体图形,那么它的俯视图是
如图是由三个小方体叠成的一个立体图形,那么它的俯视图是



 如图,正方形ABCD的边长为1,其中弧DE、弧EF、弧FG的圆心依次为点A、B、C.
如图,正方形ABCD的边长为1,其中弧DE、弧EF、弧FG的圆心依次为点A、B、C. .
.