ћвƒњƒЏ»Ё
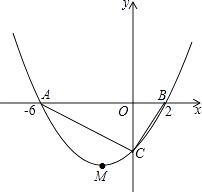
°Њћвƒњ°њ»зЌЉ1£ђ÷±ѕяy=©Б ![]() x+8£ђ”лx÷б°Ґy÷бЈ÷±рљї”ЏµгA°ҐC£ђ“‘ACќ™ґ‘љ«ѕя„чЊЎ–ќOABC£ђµгP°ҐQЈ÷±рќ™…дѕяOC°Ґ…дѕяAC…ѕµƒґѓµг£ђ«“”–AQ=2CP£ђЅђљбPQ£ђ…иµгPµƒ„ш±кќ™P£®0£ђt£©£Ѓ
x+8£ђ”лx÷б°Ґy÷бЈ÷±рљї”ЏµгA°ҐC£ђ“‘ACќ™ґ‘љ«ѕя„чЊЎ–ќOABC£ђµгP°ҐQЈ÷±рќ™…дѕяOC°Ґ…дѕяAC…ѕµƒґѓµг£ђ«“”–AQ=2CP£ђЅђљбPQ£ђ…иµгPµƒ„ш±кќ™P£®0£ђt£©£Ѓ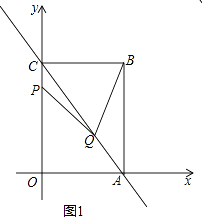
£®1£©«уµгBµƒ„ш±к£Ѓ
£®2£©»фt=1 ±£ђЅђљ”BQ£ђ«у°чABQµƒ√жїэ£Ѓ
£®3£©»зЌЉ2£ђ“‘PQќ™÷±Њґ„ч°—I£ђЉ«°—I”л…дѕяACµƒЅн“їЄцљїµгќ™E£Ѓ
Ґў»ф ![]() =
= ![]() £ђ«уіЋ ±tµƒ÷µ£Ѓ
£ђ«уіЋ ±tµƒ÷µ£Ѓ
ҐЏ»ф‘≤–ƒI‘Џ°чABCƒЏ≤њ£®≤ї∞ьЇђ±я…ѕ£©£ђ‘тіЋ ±tµƒ»°÷µЈґќІќ™ «ґа…ў?
°Њір∞Є°њ
£®1£©љв£ЇљЂx=0іъ»лy=©Б ![]() x+8£ђµ√y=8£ђ°аC£®0£ђ8£©£ђ
x+8£ђµ√y=8£ђ°аC£®0£ђ8£©£ђ
љЂy=0іъ»лy=©Б ![]() x+8£ђµ√x=6£ђ°аA£®6£ђ0£©£ђ
x+8£ђµ√x=6£ђ°аA£®6£ђ0£©£ђ
°яЋƒ±я–ќOABC «ЊЎ–ќ£ђ°аB£®6£ђ8£©
£®2£©љв£Ї»зЌЉ1£ђ

„чQH°ЌAB”ЏH£ђµ±t=1 ±£ђCP=7£ђAQ=14£ђ
“„÷§AC=10£ђsin°ѕBAC= ![]() £ђ
£ђ
°аQH=AQsin°ѕBAC= ![]() £ђ
£ђ
°аS°чABQ= ![]() £ї
£ї
£®3£©љв£ЇЈ÷ја£ЇҐс°Ґ»зЌЉ2£ђ

µ±P‘ЏѕяґќOC…ѕ£ђQ‘ЏѕяґќAC…ѕ ±£ђЉі3£Љ£Љ8 ±£ђ
“„÷§ ![]() =sin°ѕEQP=sin°ѕACO=
=sin°ѕEQP=sin°ѕACO= ![]() £ђ°а°ѕEQP=°ѕACO£ђ°аCP=PQ£ђ
£ђ°а°ѕEQP=°ѕACO£ђ°аCP=PQ£ђ
°яPE°ЌCQ£ђ°аCE=EQ£ђ°а2°Ѕ ![]() £®8©Бt£©=10©Б£®16©Б2t£©£ђљвµ√t1=
£®8©Бt£©=10©Б£®16©Б2t£©£ђљвµ√t1= ![]() £ђ
£ђ
Ґт°Ґµ±Q”лC÷ЎЇѕ£ђP‘ЏOC…ѕ ±£ђ»зЌЉ3£ђ

њ…µ√16©Б2t=10£ђљвµ√t2=3£ђ
Ґу°Ґµ±Q”лC÷ЎЇѕ£ђP‘ЏOC—”≥§ѕя…ѕ ±£ђ»зЌЉ4£ђ

њ…µ√2t©Б16=10£ђљвµ√t3=13£ђ
Ґф°Ґµ±P‘ЏOC—”≥§ѕя…ѕ£ђQ‘ЏAC—”≥§ѕя…ѕ ±£ђ»зЌЉ5£ђ

ЌђҐс£ђњ…µ√°ѕQ=°ѕPCQ£ђ
°аCP=PQ£ђ°а ![]() £®2t©Б16©Б10£©=
£®2t©Б16©Б10£©= ![]() £®t©Б8£©£ђљвµ√t4=33£ђ
£®t©Б8£©£ђљвµ√t4=33£ђ
°аt= ![]() їт3їт13їт33£ї
їт3їт13їт33£ї
ҐЏµ±‘≤–ƒI‘Џ±яAC…ѕ ±£ђ»зЌЉ6£ђP”лC÷ЎЇѕ£ђQ”лA÷ЎЇѕ£ђ
°аOP=t=8£ђ

µ±‘≤–ƒI‘Џ±яBC…ѕ ±£ђ…и°—I”лx÷бљї”ЏF£ђЅђљ”FQ£ђ
°яPQ «÷±Њґ£ђ
°аQF°Ќx÷б£ђ
°аFQ°ќOA£ђCP=CF=t©Б8£ђ
°а°чCQF°„°чACO£ђ
°а ![]() =
= ![]() £ђЉі
£ђЉі ![]() =
= ![]() £ђ
£ђ
°аt= ![]() £ђ
£ђ

°а»ф‘≤–ƒI‘Џ°чABCƒЏ≤њ£®≤ї∞ьЇђ±я…ѕ£©£ђ‘тіЋ ±tµƒ»°÷µЈґќІќ™8£Љt£Љ ![]() £ђ
£ђ
є ір∞Єќ™£Ї8£Љt£Љ ![]()
°Њљвќц°њ£®1£©љЂx=0іъ»лy=©Б ![]() x+8£ђµ√y=8£ђљЂy=0іъ»лy=©Б
x+8£ђµ√y=8£ђљЂy=0іъ»лy=©Б ![]() x+8£ђµ√x=6£ђ”Џ «µ√µљљб¬џ£ї£®2£©»зЌЉ1£ђ„чQH°ЌAB”ЏH£ђµ±t=1 ±£ђCP=7£ђAQ=14£ђљв÷±љ«»эљ«–ќµ√µљQH=AQsin°ѕBAC=
x+8£ђµ√x=6£ђ”Џ «µ√µљљб¬џ£ї£®2£©»зЌЉ1£ђ„чQH°ЌAB”ЏH£ђµ±t=1 ±£ђCP=7£ђAQ=14£ђљв÷±љ«»эљ«–ќµ√µљQH=AQsin°ѕBAC= ![]() £ђЄщЊЁ»эљ«–ќµƒ√жїэєЂ љЉіњ…µ√µљљб¬џ£ї£®3£©Ґс°Ґ»зЌЉ2£ђµ±P‘ЏѕяґќOC…ѕ£ђQ‘ЏѕяґќAC…ѕ ±£ђљв÷±љ«»эљ«–ќµ√µљљвµ√t1=
£ђЄщЊЁ»эљ«–ќµƒ√жїэєЂ љЉіњ…µ√µљљб¬џ£ї£®3£©Ґс°Ґ»зЌЉ2£ђµ±P‘ЏѕяґќOC…ѕ£ђQ‘ЏѕяґќAC…ѕ ±£ђљв÷±љ«»эљ«–ќµ√µљљвµ√t1= ![]() £ђҐт°Ґµ±Q”лC÷ЎЇѕ£ђP‘ЏOC…ѕ ±£ђ»зЌЉ3£ђљвµ√t2=3£ђҐу°Ґµ±Q”лC÷ЎЇѕ£ђP‘ЏOC—”≥§ѕя…ѕ ±£ђ»зЌЉ4£ђљвµ√t3=13£ђҐф°Ґµ±P‘ЏOC—”≥§ѕя…ѕ£ђQ‘ЏAC—”≥§ѕя…ѕ ±£ђ»зЌЉ5£ђЌђҐс£ђљвµ√t4=33£їҐЏµ±‘≤–ƒI‘Џ±яAC…ѕ ±£ђ»зЌЉ6£ђP”лC÷ЎЇѕ£ђQ”лA÷ЎЇѕ£ђ«уµ√OP=t=8£ђµ±‘≤–ƒI‘Џ±яBC…ѕ ±£ђ…и°—I”лx÷бљї”ЏF£ђЅђљ”FQ£ђЄщЊЁѕаЋ∆»эљ«–ќµƒ–‘÷ µ√µљt=
£ђҐт°Ґµ±Q”лC÷ЎЇѕ£ђP‘ЏOC…ѕ ±£ђ»зЌЉ3£ђљвµ√t2=3£ђҐу°Ґµ±Q”лC÷ЎЇѕ£ђP‘ЏOC—”≥§ѕя…ѕ ±£ђ»зЌЉ4£ђљвµ√t3=13£ђҐф°Ґµ±P‘ЏOC—”≥§ѕя…ѕ£ђQ‘ЏAC—”≥§ѕя…ѕ ±£ђ»зЌЉ5£ђЌђҐс£ђљвµ√t4=33£їҐЏµ±‘≤–ƒI‘Џ±яAC…ѕ ±£ђ»зЌЉ6£ђP”лC÷ЎЇѕ£ђQ”лA÷ЎЇѕ£ђ«уµ√OP=t=8£ђµ±‘≤–ƒI‘Џ±яBC…ѕ ±£ђ…и°—I”лx÷бљї”ЏF£ђЅђљ”FQ£ђЄщЊЁѕаЋ∆»эљ«–ќµƒ–‘÷ µ√µљt= ![]() £ђ”Џ «µ√µљљб¬џ£Ѓ
£ђ”Џ «µ√µљљб¬џ£Ѓ
°ЊњЉµгЊЂќц°њ±Њћв÷ч“™њЉ≤йЅЋѕаЋ∆»эљ«–ќµƒ”¶”√µƒѕаєЎ÷™ ґµг£ђ–и“™’∆ќ’≤вЄя£Ї≤вЅњ≤їƒ№µљіпґ•≤њµƒќпћеµƒЄяґ»£ђЌ®≥£”√°∞‘ЏЌђ“ї ±њћќпЄя”л”∞≥§≥…±»јэ°±µƒ‘≠јнљвЊц£ї≤вЊа£Ї≤вЅњ≤їƒ№µљіпЅљµгЉдµƒЊўјэ£ђ≥£єє‘мѕаЋ∆»эљ«–ќ«уљв≤≈ƒ№’э»ЈљвіріЋћв£Ѓ

°Њћвƒњ°њќ™ЅЋЉ”«њєЂ√сµƒљЏЋЃ“в ґ£ђЇѕјнјы”√ЋЃ„ ‘і£ђƒ≥ –≤…”√ЉџЄсµчњЎ ÷ґќіпµљљЏЋЃµƒƒњµƒ£ђЄ√ –„‘јіЋЃ ’Ј—ЉџЄсЉыЉџƒњ±н£Ѓ
Љџƒњ±н
√њ‘¬ЋЃ”√Ѕњ | µ•Љџ |
≤ї≥ђ≥ц |
|
≥ђ≥ц |
|
≥ђ≥ц |
|
„Ґ£ЇЋЃЈ—∞і‘¬љбЋг.
»фƒ≥їІЊ”√с![]() ‘¬ЈЁ”√ЋЃ
‘¬ЈЁ”√ЋЃ![]() £ђ‘т”¶ ’ЋЃЈ—£Ї
£ђ‘т”¶ ’ЋЃЈ—£Ї![]() ‘™£Ѓ
‘™£Ѓ
£®1£©»фЄ√їІЊ”√с![]() ‘¬ЈЁ”√ЋЃ
‘¬ЈЁ”√ЋЃ![]() £ђ‘т”¶ ’ЋЃЈ—_______‘™£ї
£ђ‘т”¶ ’ЋЃЈ—_______‘™£ї
£®2£©»фЄ√їІЊ”√с![]() °Ґ
°Ґ![]() ‘¬ЈЁє≤”√ЋЃ
‘¬ЈЁє≤”√ЋЃ![]() £®
£®![]() ‘¬ЈЁ”√ЋЃЅњ≥ђєэ
‘¬ЈЁ”√ЋЃЅњ≥ђєэ![]() ‘¬ЈЁ£©£ђє≤љїЋЃЈ—
‘¬ЈЁ£©£ђє≤љїЋЃЈ—![]() ‘™£ђ‘тЄ√їІЊ”√с
‘™£ђ‘тЄ√їІЊ”√с![]() ‘¬ЈЁЄч”√ЋЃґа…ўЅҐЈљ√„£њ
‘¬ЈЁЄч”√ЋЃґа…ўЅҐЈљ√„£њ