题目内容
在等腰△ABC中,三边分别为a、b、c,其中a=4,b、c恰好是方程 的两个实数根,则△ABC的周长为__________.
的两个实数根,则△ABC的周长为__________.
10
解析试题分析:题目中没有明确腰和底,故要分情况讨论,同时结合一元二次方程根的判别式求解即可.
当腰为4时,方程 有一根也为4
有一根也为4
所以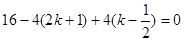 ,解得
,解得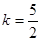
则原方程可化为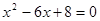 ,解得
,解得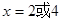
此时等腰△ABC的三边分别为4、4、2,则周长为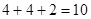
当底为4时,方程 有两个相等的实数根
有两个相等的实数根
所以△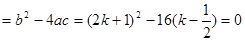 ,解得
,解得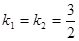
则原方程可化为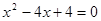 ,解得
,解得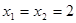
此时等腰△ABC的三边分别为4、2、2,无法构成三角形,舍去
综上,△ABC的周长为10.
考点:等腰三角形的性质,一元二次方程根的判别式
点评:解答本题的关键是熟练掌握一元二次方程根的情况与判别式△ 的关系:(1)
的关系:(1) 方程有两个不相等的实数根;(2)
方程有两个不相等的实数根;(2) 方程有两个相等的实数根;(3)
方程有两个相等的实数根;(3) 方程没有实数根.
方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
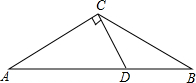 如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D. 如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,且3BC=2AD.点E、F是AD的三等分点,则∠BEC+∠BFC+∠BAC=
如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,且3BC=2AD.点E、F是AD的三等分点,则∠BEC+∠BFC+∠BAC= 如图,在等腰△ABC中,AB=AC,B(
如图,在等腰△ABC中,AB=AC,B( 在等腰△ABC中,AB=AC=13,BC=10,取BC所在的直线为x轴,且点B为原点建立直角坐标系.
在等腰△ABC中,AB=AC=13,BC=10,取BC所在的直线为x轴,且点B为原点建立直角坐标系.