题目内容
如图，E是矩形ABCD的AB边上任意一点，F是AD边上一点，∠EFC=90°，图中一定相似的三角形是
- A.①与②
- B.③与④
- C.②与③
- D.①与④
A
分析：由矩形ABCD，根据矩形的四个角都等于90°，可得∠A=∠D=90°；根据直角三角形的两锐角互余，可得∠AEF+∠AFE=90°；又由∠EFC=90°，根据同角的余角相等，可得∠CFD=∠AEF；根据有两个角对应相等的三角形相似，可得△AEF∽△DFC．
解答：∵四边形ABCD是矩形，
∴∠A=∠D=90°，
∵∠EFC=90°，
∴∠AEF+∠AFE=90°，∠AFE+∠DFC=90°，
∴∠AEF=∠DFC，
∴△AEF∽△DFC．
故选A．
点评：此题考查了矩形的性质、直角三角形的性质、三角形相似的判定等知识．解题的关键是认真审题，注意相似三角形的判定：有两个角对应相等的三角形相似；注意同角的余角相等．
分析：由矩形ABCD，根据矩形的四个角都等于90°，可得∠A=∠D=90°；根据直角三角形的两锐角互余，可得∠AEF+∠AFE=90°；又由∠EFC=90°，根据同角的余角相等，可得∠CFD=∠AEF；根据有两个角对应相等的三角形相似，可得△AEF∽△DFC．
解答：∵四边形ABCD是矩形，
∴∠A=∠D=90°，
∵∠EFC=90°，
∴∠AEF+∠AFE=90°，∠AFE+∠DFC=90°，
∴∠AEF=∠DFC，
∴△AEF∽△DFC．
故选A．
点评：此题考查了矩形的性质、直角三角形的性质、三角形相似的判定等知识．解题的关键是认真审题，注意相似三角形的判定：有两个角对应相等的三角形相似；注意同角的余角相等．
练习册系列答案
智慧小复习系列答案
相关题目
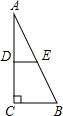如图，在一张△ABC纸片中，∠C=90°，∠B=60°，DE是中位线，现把纸片沿中位线DE剪开，计划拼出以下四个图形：①邻边不等的矩形；②等腰梯形；③有两个角为锐角的菱形；④正方形．那么以上图形一定能被拼成的个数为（ ）
