Question

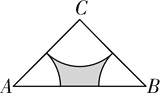
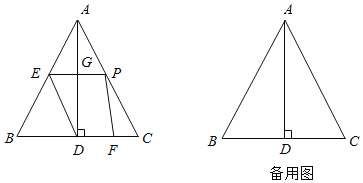
【题目】已知：如图，在等边△ABC中，AB＝6cm，AD⊥BC于点D，动点F从点C出发，沿CB方向以1cm/s的速度向点D运动；同时，动点P也从点C出发，沿CA方向以3cm/s的速度向点A运动，过点P作PE∥BC，与边AB交于点E，与AD交于点G，连结ED，PF．设运动的时间为t（s）（0＜t＜2）．

（1）当t为何值时，四边形EDFP为平行四边形？

（2）设四边形EDFP面积为y，求y与t之间的函数关系式；

（3）连结PD、EF，当t为何值时，PD⊥EF？

Answer 1

【答案】（1）s；（2）y＝﹣3t2+t；（3）当t＝s时，PD⊥EF．

【解析】

（1）根据已知条件可推出△APE是等边三角形，由题意可得CP＝3t，CF＝t，则AP＝6﹣3t，PE＝6﹣3t，DF＝DC﹣CF＝3﹣t，根据四边形EDFP为平行四边形，列出方程求解即可得出答案；

（2）过点P作PH⊥BC于H，根据现有条件得出PH＝t，再根据y＝S△ABC﹣S△APE﹣S△PCF﹣S△EDB即可得出解析式；

（3）设PD交EF于点O，过点E作EH⊥BC于H，根据已知条件推出PG＝EG＝PE＝（6﹣3t），同（2）得：EH＝t，BH＝t，推出∠PDG＝∠OFD，即tan∠PDG＝tan∠OFD＝＝，据此列式求解即可．

解：（1）∵等边△ABC中，AB＝6cm，AD⊥BC，

∴AC＝AB＝BC＝6，DC＝BD＝BC＝3，∠B＝∠C＝60°，

∵PE∥BC，

∴∠APE＝∠AEP＝∠B＝∠C＝60°，

∴△APE是等边三角形，

∴AP＝PE，

由题意得：CP＝3t，CF＝t，则AP＝6﹣3t，

∴PE＝6﹣3t，DF＝DC﹣CF＝3﹣t，

∵四边形EDFP为平行四边形，

∴PE＝DF，

∴6﹣3t＝3﹣t，

∴t＝，

∴当t＝s时，四边形EDFP为平行四边形；

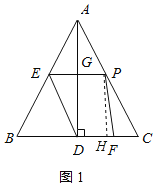
（2）过点P作PH⊥BC于H，如图1所示：

由勾股定理得：AD＝＝＝3，

∵∠C＝60°，

∴sin60°＝＝，

∴PH＝×3t＝t，

∵PE∥BC，AD⊥BC，PH⊥BC，

∴四边形PGDH是矩形，

∴PH＝DG，

∴y＝S△ABC﹣S△APE﹣S△PCF﹣S△EDB

＝ADBC﹣（AD﹣PH）PE﹣PHCF﹣PHBD

＝×3×6﹣×（3t）×（6﹣3t）﹣×t×t﹣×t×3

＝﹣3t2+t；

（3）设PD交EF于点O，过点E作EH⊥BC于H，如图2所示：

则四边形EHDG是矩形，

∴EH＝DG，

∵△APE是等边三角形，

∴PG＝EG＝PE＝（6﹣3t），

同（2）得：EH＝t，BH＝t，

∵PD⊥EF，

∴∠FOD＝90°，

∴∠OFD+∠ODF＝90°，

∵∠ODF+∠PDG＝90°，

∴∠PDG＝∠OFD，

∴tan∠PDG＝tan∠OFD＝＝，

∴＝，

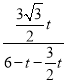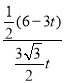∴2t2+11t﹣12＝0，

解得：t1＝，t2＝（不合题意舍去），

则当t＝s时，PD⊥EF．