题目内容
如图,矩形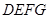 的边
的边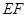 在
在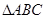 的边
的边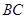 上,顶点
上,顶点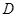 、
、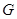 分别在边
分别在边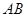 、
、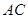 上,
上,
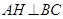 ,垂足为
,垂足为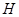 .已知
.已知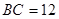 ,
,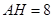 .
.
(1)当矩形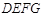 为正方形时,求该正方形的边长;
为正方形时,求该正方形的边长;
(2)当矩形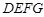 面积为18时,求矩形的长和宽.
面积为18时,求矩形的长和宽.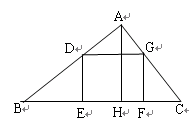
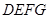 的边
的边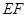 在
在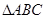 的边
的边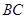 上,顶点
上,顶点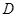 、
、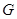 分别在边
分别在边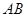 、
、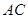 上,
上,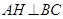 ,垂足为
,垂足为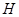 .已知
.已知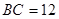 ,
,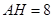 .
.(1)当矩形
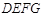 为正方形时,求该正方形的边长;
为正方形时,求该正方形的边长;(2)当矩形
 面积为18时,求矩形的长和宽.
面积为18时,求矩形的长和宽.
解:(1)记AH与DG的交点为H,设正方形边长为x,
∵正方形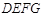 ,EF在边BC上
,EF在边BC上
∴DG∥BC
得△ADG∽△ABC
∴
由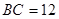
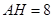
可得
∴
(2)设
可得
即
∵矩形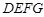 面积为18
面积为18
即
∴
解得
当 时,
时, ;当
;当 时,
时,
∴矩形的长宽分别为2、9或6、3
∵正方形
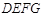 ,EF在边BC上
,EF在边BC上∴DG∥BC
得△ADG∽△ABC
∴

由
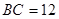
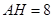
可得

∴

(2)设

可得

即

∵矩形
 面积为18
面积为18即

∴

解得

当
 时,
时, ;当
;当 时,
时,
∴矩形的长宽分别为2、9或6、3
(1)DG∥BC得△ADG∽△ABC,利用相似三角形对应边上高的比等于相似比,列方程求解.
(2)设DE=a,DG=b,利用相似三角形得到 ,再根据矩形DEFG面积为18列出方程
,再根据矩形DEFG面积为18列出方程 求得a值代入求得b值即可.
求得a值代入求得b值即可.
(2)设DE=a,DG=b,利用相似三角形得到
 ,再根据矩形DEFG面积为18列出方程
,再根据矩形DEFG面积为18列出方程 求得a值代入求得b值即可.
求得a值代入求得b值即可.
练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 中,
中, 是
是 边上一点,过点
边上一点,过点 作
作 交
交 于点
于点 过点
过点 作
作 交
交 于点
于点 则四边形
则四边形 的周长是_________.
的周长是_________.
 中,
中, ∥
∥ ,
, ,
, ,
, ,则梯形
,则梯形


 中,
中, ,对角线BD=7,则菱形
,对角线BD=7,则菱形
 ?
?
