题目内容
 如图,△ABC的∠B,∠C的外角的平分线交于点P.
如图,△ABC的∠B,∠C的外角的平分线交于点P.(1)若∠ABC=50°,∠A=70°,则∠P=
(2)若∠ABC=48°,∠A=70°,则∠P=
(3)若∠A=68°,则∠P=
(4)根据以上计算,试写出∠P与∠A的数量关系:
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)(2)根据三角形的内角和等于180°求出∠ACB,再根据邻补角的定义和角平分线的定义求出∠PBC和∠PCB,然后利用三角形的内角和定理列式计算即可得解;
(3)根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠PBC+∠PCB,再利用三角形的内角和定理列式整理可得∠P=90°-
∠A;
(4)根据计算结果写出即可.
(3)根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠PBC+∠PCB,再利用三角形的内角和定理列式整理可得∠P=90°-
| 1 |
| 2 |
(4)根据计算结果写出即可.
解答:解:(1)∵∠ABC=50°,∠A=70°,
∴∠ACB=180°-50°-70°=60°,
∵∠B,∠C的外角的平分线交于点P,
∴∠PBC=
(180°-50°)=65°,∠PCB=
(180°-60°)=60°,
在△PBC中,∠P=180°-65°-60°=55°;
(2)∵∠ABC=48°,∠A=70°,
∴∠ACB=180°-48°-70°=62°,
∵∠B,∠C的外角的平分线交于点P,
∴∠PBC=
(180°-48°)=66°,∠PCB=
(180°-62°)=59°,
在△PBC中,∠P=180°-66°-59°=55°;
(3)∵∠B,∠C的外角的平分线交于点P,
∴∠PBC+∠PCB=
(∠A+∠ACB)+
(∠A+∠ABC),
=
(∠A+∠ACB+∠ABC+∠A),
=
(180°+∠A),
=90°+
∠A,
在△PBC中,∠P=180°-(∠PBC+∠PCB)=180°-(90°+
∠A)=90°-
∠A;
∵∠A=68°,
∴∠P=90°-34=56°;
(4)∠P=90°-
∠A.
故答案为:(1)55;(2)55;(3)56;(4)∠P=90°-
∠A.
∴∠ACB=180°-50°-70°=60°,
∵∠B,∠C的外角的平分线交于点P,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
在△PBC中,∠P=180°-65°-60°=55°;
(2)∵∠ABC=48°,∠A=70°,
∴∠ACB=180°-48°-70°=62°,
∵∠B,∠C的外角的平分线交于点P,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
在△PBC中,∠P=180°-66°-59°=55°;
(3)∵∠B,∠C的外角的平分线交于点P,
∴∠PBC+∠PCB=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
在△PBC中,∠P=180°-(∠PBC+∠PCB)=180°-(90°+
| 1 |
| 2 |
| 1 |
| 2 |
∵∠A=68°,
∴∠P=90°-34=56°;
(4)∠P=90°-
| 1 |
| 2 |
故答案为:(1)55;(2)55;(3)56;(4)∠P=90°-
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的角平分线的定义,利用整体思想推出(3)的结论是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
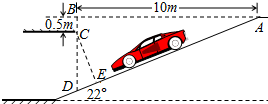 如图是某超市地下停车场入口的设计图,请根据图中数据计算CE的长度.(结果保留小数点后两位;参考数据:sin22°=0.3746,cos22°=0.9272,tan22°=0.4040)
如图是某超市地下停车场入口的设计图,请根据图中数据计算CE的长度.(结果保留小数点后两位;参考数据:sin22°=0.3746,cos22°=0.9272,tan22°=0.4040)