题目内容

精英家教网在等边△ABC中，点D，E分别在边BC，AB上，且BD=AE．求证：AD=CE．
分析：在等边△ABC中，AC=BA，∠EAC=∠DBA，且BD=AE则可得出△CAE≌△ABD从而得出AD=CE．
解答：证明：在△ABC中CA=AB，∠CAE=∠ABD，
又∵AE=BD，
在△CAE和△ABD中，
AE=BD
∠B=∠CAE
CA=AB
，
∴△CAE≌△ABD（SAS）．
∴AD=CE．
点评：本题考查了等边三角形的性质和全等三角形的判定与性质；三角形全等的证明是正确解答本题的关键．
练习册系列答案
相关题目
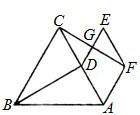22、如图，在等边△ABC中，点D为AC中点，以AD为边作菱形ADEF，且AF∥BC，连接FC交DE于点G．
（1）求证：△ADB≌△AFC；
（2）写出图中除（1）以外的两对全等三角形（不要求写证明过程）．
在等边△ABC中，点D为AC上一点，连接BD，直线l与AB，BD，BC分别相交于点E，P，F，且∠BPF=60度．
（1）如图1，写出图中所有与△BPF相似的三角形，并选择其中一对给予证明；
（2）若直线l向右平移到图2，图3的位置时（其它条件不变），（1）中的结论是否仍然成立？若成立，请写出来（不证明），若不成立，请说明理由；
（3）探究：如图1，当BD满足什么条件时（其它条件不变），PF=
12
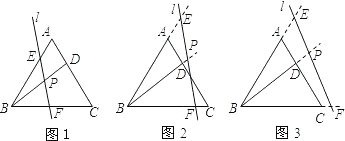PE？请写出探精英家教网究结果，并说明理由．
（说明：结论中不得含有未标识的字母）
在等边△ABC中，点D为AC上一点，连接BD，直线l与线段BA、BD、BC分别相交于点E、P、F，且∠BPF=60°．
（1）如图1，写出图中所有与△BDC相似的三角形，并选择其中一对给予证明；
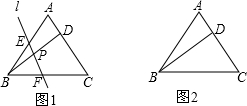
（2）若直线l向右平移，与线段BA、BD、BC或其延长线分别相交于E、P、F，请在图2中画出一个与图1位置不尽相同的图形（其它条件不变），此时，（1）中的结论是否仍然成立？若成立，请写出来（不证明），若不成立，请说明理由；精英家教网
（3）探究：如图1，当BD满足什么条件时（其它条件不变），△BPE的面积是△BPF的面积的2倍？请写出探究结果，并说明理由．（说明：结论中不得含有未标识的字母）．
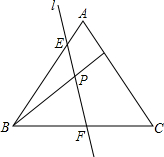如图，在等边△ABC中，点D为AC上一点，连结AB，BD，BC分别相交于点E，P，F，且∠BPF=60°
（1）写出图中所有与△BPF相似的三角形，并选择其中一对给予证明；
（2）探究：当BD什么条件时（其它条件不变），PF=
12
PE？请写出探究结果，并说明理由．（说明：结论中不得含有未标识的字母）
已知：如图，在等边△ABC中取点P，使得PA，PB，PC的长分别为3，4，5，将线段AP以点A为旋转中心顺时针旋转60°到线段AD，连接BD，下列结论：
①△ABD可以由△APC绕点A顺时针旋转60°得到；②点P与点D的距离为3；③∠APB=150°；④S△APC+S△APB=6+
9
4
3
．
其中正确的结论有（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网