题目内容
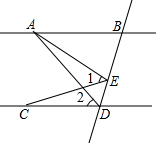已知AB∥CD，AB=AD，EA=EC，求证：∠1=∠2．考点：四点共圆,平行线的性质,全等三角形的判定与性质,等腰三角形的性质,圆周角定理
专题：证明题
分析：在CD的延长线上取一点F，使得DF=DA，如图所示．由AB∥CD，AB=AD可得到∠ADB=∠FDB，即可证到△ADE≌△FDE，则有EA=EF，∠EAD=∠EFD，由EA=EC可得EC=EF，从而有∠ECD=∠EFD，从而可得∠ECD=∠EAD，进而可得点E、A、C、D四点共圆，然后根据圆周角定理就可得到∠1=∠2．
解答：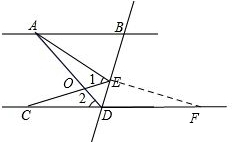
解：在CD的延长线上取一点F，使得DF=DA，如图所示．
∵AB∥CD，∴∠ABD=∠FDB．
∵AB=AD，∴∠ABD=∠ADB．
∴∠ADB=∠FDB．
在△ADE和△FDE中，
，
∴△ADE≌△FDE（SAS），
∴EA=EF，∠EAD=∠EFD．
∵EA=EC，∴EC=EF，
∴∠ECD=∠EFD，
∴∠ECD=∠EAD，
∴点E、A、C、D四点共圆，
∴∠1=∠2．
解：在CD的延长线上取一点F，使得DF=DA，如图所示．∵AB∥CD，∴∠ABD=∠FDB．
∵AB=AD，∴∠ABD=∠ADB．
∴∠ADB=∠FDB．
在△ADE和△FDE中，
|
∴△ADE≌△FDE（SAS），
∴EA=EF，∠EAD=∠EFD．
∵EA=EC，∴EC=EF，
∴∠ECD=∠EFD，
∴∠ECD=∠EAD，
∴点E、A、C、D四点共圆，
∴∠1=∠2．
点评：本题考查了平行线的性质、等腰三角形的性质、全等三角形的判定与性质、四点共圆的判定、圆周角定理等知识，而解决本题的关键是利用角平分线构造全等三角形．另外，证到∠ECD=∠EAD后，也可利用三角形外角的性质（∠AOC=∠EAO+∠1=∠DCO+∠2）证到∠1=∠2．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
在矩形ABCD中，AB=5cm，BC=10cm，点P从点A沿矩形的边以1cm/s的速度经B向C运动，点Q从B点出发沿矩形的边以2cm/s的速度经C向D运动，点P、Q同时运动，且一点到达终点另一点也停止运动，求几秒后以P、Q、B为顶点的三角形的面积等于6平方厘米？