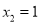��Ŀ����
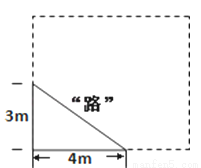
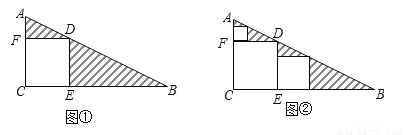
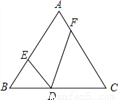
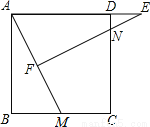
������ֽƬABC�У���C=90�㣬AC=1��BC=2����ͼ�ٵķ�ʽ������ֽƬ�м�ȥһ�������ܴ�������Σ���Ϊ��1�μ�ȡ�������µ����������������ΪS1����ͼ�ڵķ�ʽ�����µ�Rt��ADF��Rt��BDE�У��ֱ��ȥ�����ܴ�������Σ���Ϊ��2�μ�ȡ�������µ����������������ΪS2������������ȥ������
��1����ͼ�٣���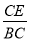 ��S1��ֵ��
��S1��ֵ��
��2����n�μ�ȡ�����µ��������������֮��SnΪ________��
��ϰ��ϵ�д�
�����Ŀ
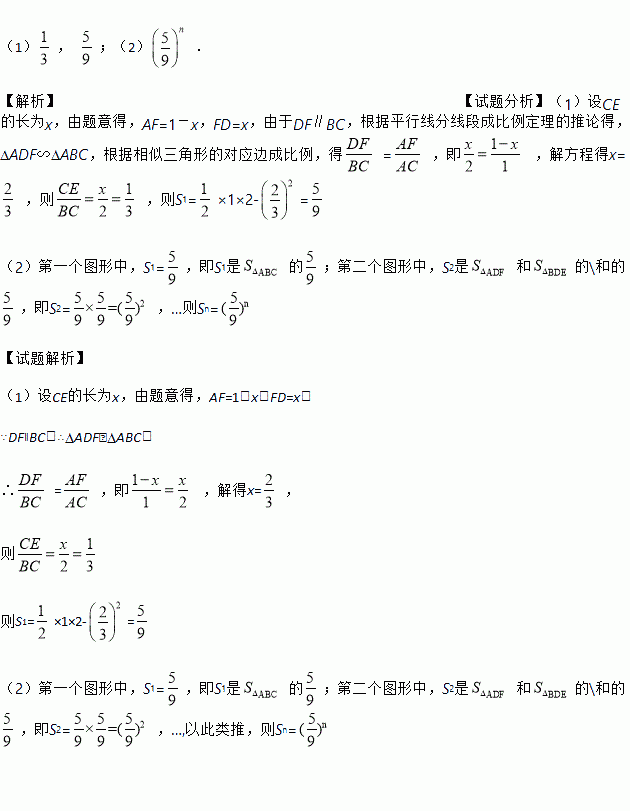

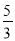
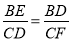 ������֪�ã�CD=BC-BD=5-1=4���ɴ˿ɵã�
������֪�ã�CD=BC-BD=5-1=4���ɴ˿ɵã� 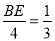 �����BE=
�����BE=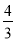 .
.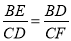 ����
����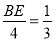 ��
��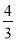 .
.
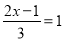 �Ľ���____��
�Ľ���____��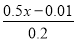 ��0.5=
��0.5=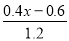 �ķ�ĸ��Ϊ��������ȷ���ǣ�������
�ķ�ĸ��Ϊ��������ȷ���ǣ�������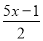 ��0.5=
��0.5=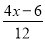 B.
B. 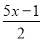 ��0.5=
��0.5=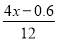
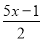 ��0.5=
��0.5=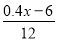 D.
D. 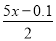 ��0.5=
��0.5=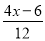
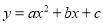 �ĶԳ���Ϊֱ��x=��1����y�ཻ�ڣ�0����6���������x�ķ���
�ĶԳ���Ϊֱ��x=��1����y�ཻ�ڣ�0����6���������x�ķ���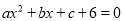 �Ľ�Ϊ��������
�Ľ�Ϊ��������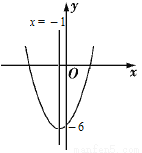
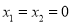 B.
B. 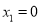 ��
�� 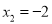
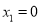 ��
�� 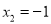 D.
D. 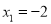 ��
��