题目内容
 如图,将半径为1的圆形纸板,沿长、宽分别为8和5的矩形的外侧滚动一周并回到开始的位置,则圆心所经过的路线长度是
如图,将半径为1的圆形纸板,沿长、宽分别为8和5的矩形的外侧滚动一周并回到开始的位置,则圆心所经过的路线长度是
- A.13
- B.26
- C.13+π
- D.26+2π
D
分析:根据圆与矩形的边相切,则圆从一边滚到另一边,圆心都要绕其矩形的顶点旋转90°,得到圆心绕其矩形的四个顶点共旋转了360°,根据弧长公式可计算出圆心旋转的弧长,再加上矩形的周长即可得到圆心所经过的路线长度.
解答:∵圆从一边滚到另一边,圆心都要绕其矩形的顶点旋转90°,
∴圆心绕其矩形的四个顶点共旋转了360°,
∴圆沿矩形的外侧滚动一周并回到开始的位置,则圆心所经过的路线长度=8+8+5+5+ =26+2π.
=26+2π.
故选D.
点评:本题考查了弧长公式:l= (n为圆心角,R为半径);也考查了旋转的性质.
(n为圆心角,R为半径);也考查了旋转的性质.
分析:根据圆与矩形的边相切,则圆从一边滚到另一边,圆心都要绕其矩形的顶点旋转90°,得到圆心绕其矩形的四个顶点共旋转了360°,根据弧长公式可计算出圆心旋转的弧长,再加上矩形的周长即可得到圆心所经过的路线长度.
解答:∵圆从一边滚到另一边,圆心都要绕其矩形的顶点旋转90°,
∴圆心绕其矩形的四个顶点共旋转了360°,
∴圆沿矩形的外侧滚动一周并回到开始的位置,则圆心所经过的路线长度=8+8+5+5+
 =26+2π.
=26+2π.故选D.
点评:本题考查了弧长公式:l=
 (n为圆心角,R为半径);也考查了旋转的性质.
(n为圆心角,R为半径);也考查了旋转的性质. 
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 11、如图,将半径为1的圆的边上的A点与数轴的原点重合,然后沿着数轴向右滚动,滚动一周得到点A′,则点A′表示的数为
11、如图,将半径为1的圆的边上的A点与数轴的原点重合,然后沿着数轴向右滚动,滚动一周得到点A′,则点A′表示的数为

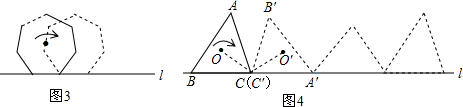
 如图,将半径为1的圆的边上的A点与数轴的原点重合,然后沿着数轴向右滚动,滚动一周得到点A′,则点A′表示的数为________.
如图,将半径为1的圆的边上的A点与数轴的原点重合,然后沿着数轴向右滚动,滚动一周得到点A′,则点A′表示的数为________.

 cm
cm cm
cm cm
cm cm
cm