Question

如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点H处，点D落在点G处，则线段BF的取值范围为　　．

Answer 1

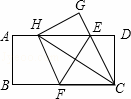
3≤BF≤4 解：如图1，当点H与点A重合时，

∵四边形ABCD为矩形，

∴∠B=90°；

由题意得：AF=CF（设为λ），则BF=8﹣λ；

由勾股定理得：λ²=4²+（8﹣λ）²，

解得：λ=5，BF=3；

如图2，当点E与点D重合时，

由翻折变换的性质得：∠HEF=∠CEF=45°，HE=CE；

∴∠CEF=∠CFE，

∴CF=CE=4，BF=8﹣4=4，

综上所述，线段BF的取值范围为3≤BF≤4．

故答案为3≤BF≤4．