题目内容
 如图一个直角三角形PQR的直角顶点为Q,以其三边为直径作三个半圆,矩形STUV的各边与半圆相切且平行于PQ或者QR.如果PQ=6厘米,QR=8厘米,则STUV的面积是多少平方厘米?
如图一个直角三角形PQR的直角顶点为Q,以其三边为直径作三个半圆,矩形STUV的各边与半圆相切且平行于PQ或者QR.如果PQ=6厘米,QR=8厘米,则STUV的面积是多少平方厘米?分析:首先取PR的中点O,过点O作MN∥ST,EF∥SV,由题意可得MN⊥SV、MN⊥TU、EF⊥ST、EF⊥VU;EL、KN、OM、OF分别是各半圆的半径,OL和OK是△ABC的中位线,又由在Rt△PQR中,PQ=6厘米,QR=8厘米,即可求得各个线段的长,继而求得答案.
解答:解:取PR的中点O,过点O作MN∥ST,EF∥SV,

∵四边形STUV是矩形,
∴SV∥EF∥TU,ST∥MN∥UV,∠S=∠V=90°,
∴MN⊥SV、MN⊥TU、EF⊥ST、EF⊥VU,
∵PQ∥ST,QR∥TU,
∴PQ∥MN∥VU,QR∥EF∥TU,
∴PL=QL,QK=RK,
∴OL=
QR=
×8=4,OK=
PQ=
×6=3厘米,
∵矩形STUV的各边分别与半圆相切,
∴EL=
PQ=
×6=3,KN=
QR=
×8=4厘米,
在Rt△PQR中,PR=
=10厘米,
∴OM=OF=
×PR=5厘米,
∴SV=FU=EF=EL+OL+OF=3+4+5=12厘米,ST=UV=MN=OM+OK+NK=5+3+4=12厘米,
∴S矩形STUV=12×12=144平方厘米.

∵四边形STUV是矩形,
∴SV∥EF∥TU,ST∥MN∥UV,∠S=∠V=90°,
∴MN⊥SV、MN⊥TU、EF⊥ST、EF⊥VU,
∵PQ∥ST,QR∥TU,
∴PQ∥MN∥VU,QR∥EF∥TU,
∴PL=QL,QK=RK,
∴OL=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵矩形STUV的各边分别与半圆相切,
∴EL=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△PQR中,PR=
| 62+82 |
∴OM=OF=
| 1 |
| 2 |
∴SV=FU=EF=EL+OL+OF=3+4+5=12厘米,ST=UV=MN=OM+OK+NK=5+3+4=12厘米,
∴S矩形STUV=12×12=144平方厘米.
点评:此题考查了切线的性质、矩形的性质,三角形中位线的性质以及勾股定理等知识.此题难度较大,解题的关键是掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
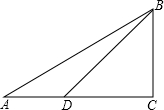 如图,直角三角形三边长AB=10cm,AC=ycm,BC=xcm.
如图,直角三角形三边长AB=10cm,AC=ycm,BC=xcm.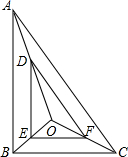 如图,直角三角形ABC到直角三角形DEF是一个相似变换,AC与DF的长度之比是3:2.
如图,直角三角形ABC到直角三角形DEF是一个相似变换,AC与DF的长度之比是3:2. 如图一个直角三角形PQR的直角顶点为Q,以其三边为直径作三个半圆,矩形STUV的各边与半圆相切且平行于PQ或者QR.如果PQ=6厘米,QR=8厘米,则STUV的面积是多少平方厘米?
如图一个直角三角形PQR的直角顶点为Q,以其三边为直径作三个半圆,矩形STUV的各边与半圆相切且平行于PQ或者QR.如果PQ=6厘米,QR=8厘米,则STUV的面积是多少平方厘米?