题目内容
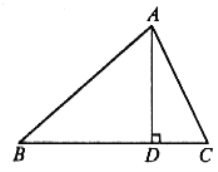
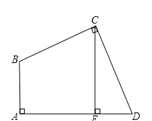
【题目】如图,在平面直角坐标系![]() 中,已知△ABC,∠ABC=90°,顶点A在第一象限,顶点B、C在x轴的正半轴上(C在B的右侧),
中,已知△ABC,∠ABC=90°,顶点A在第一象限,顶点B、C在x轴的正半轴上(C在B的右侧),![]() ,△ADC与△ABC关于AC所在的直线对称.
,△ADC与△ABC关于AC所在的直线对称.
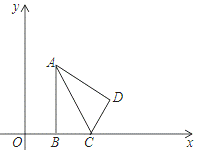
(1)当OB=2时,求点D的坐标.
(2)若点![]() 和点
和点![]() 在同一个反比例函数图象上,求
在同一个反比例函数图象上,求![]() 的长.
的长.
【答案】(1)点![]() 的坐标是
的坐标是![]() ;(2)
;(2)![]() 的长为3
的长为3
【解析】
(1)过点![]() 作
作![]() 轴于点
轴于点![]() ,利用∠ACB的正切值可求出∠ACB的度数,根据轴对称的性质可得DC=BC,∠ACD=∠ACB,利用平角定义可求出∠DCE的度数,利用∠DCE的三角函数可求出CE和DE的长,根据OE=OB+BC+CE可求出OE,即可得点D坐标;(2)设
,利用∠ACB的正切值可求出∠ACB的度数,根据轴对称的性质可得DC=BC,∠ACD=∠ACB,利用平角定义可求出∠DCE的度数,利用∠DCE的三角函数可求出CE和DE的长,根据OE=OB+BC+CE可求出OE,即可得点D坐标;(2)设![]() ,可用a表示出点A坐标,由(1)得CE、DE的长,可用a表示出点D坐标,根据反比例函数图象上点的坐标特征列方程求出a的值即可得答案.
,可用a表示出点A坐标,由(1)得CE、DE的长,可用a表示出点D坐标,根据反比例函数图象上点的坐标特征列方程求出a的值即可得答案.
(1)如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵△ADC与△ABC关于AC所在的直线对称,
∴DC=BC=2,∠ACD=∠ACB=60°,
∴∠DCE=180°-60°-60°=60°,
∴CE=CD·cos∠DCE=1,DE=CD·sin∠DCE=![]() ,
,
∴![]() ,
,
∴点![]() 的坐标是
的坐标是![]() .
.

(2)设![]() ,则点
,则点![]() 的坐标是
的坐标是![]() ,
,
由(1)得:![]() ,
,
∵BC=2,
∴OE=a+2+1=3+a,
∴点![]() 的坐标是
的坐标是![]() ,
,
∵点![]() 和点
和点![]() 在同一个反比例函数的图象上,
在同一个反比例函数的图象上,
∴![]() ,
,
解得:![]() ,即
,即![]() 的长为3.
的长为3.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目