题目内容
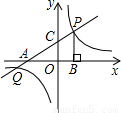
如图,直线 分别交x轴、y轴于A、B两点,线段AB的垂直平分线分别交x轴、y轴于C、D两点.
分别交x轴、y轴于A、B两点,线段AB的垂直平分线分别交x轴、y轴于C、D两点.(1)求点C的坐标;
(2)求△BCD的面积.

【答案】分析:(1)由直线y=- x+8,分别交x轴、y轴于A、B两点,即可求得点A与B的坐标,即可得OA,OB,由勾股定理即可求得AB的长,由CD是线段AB的垂直平分线,可求得AE与BE的长,易证得△AOB∽△AEC,然后由相似三角形的对应边成比例,即可求得AC的长,继而求得点C的坐标;
x+8,分别交x轴、y轴于A、B两点,即可求得点A与B的坐标,即可得OA,OB,由勾股定理即可求得AB的长,由CD是线段AB的垂直平分线,可求得AE与BE的长,易证得△AOB∽△AEC,然后由相似三角形的对应边成比例,即可求得AC的长,继而求得点C的坐标;
(2)易证得△AOB∽△DEB,由相似三角形的对应边成比例,即可求得BD的长,又由S△BCD= BD•OC,即可求得△BCD的面积.
BD•OC,即可求得△BCD的面积.
解答:解:(1)∵直线y=- x+8,分别交x轴、y轴于A、B两点,
x+8,分别交x轴、y轴于A、B两点,
当x=0时,y=8;当y=0时,x=6.
∴OA=6,OB=8.
在Rt△AOB中,AB= =10,
=10,
∵CD是线段AB的垂直平分线,
∴AE=BE=5.
∵∠OAB=∠CAE,∠AOB=∠AEC=90°,
∴△AOB∽△AEC,
∴ ,
,
即 ,
,
∴AC= .
.
∴OC=AC-OA= ,
,
∴点C的坐标为(- ,0);
,0);
(2)∵∠ABO=∠DBE,∠AOB=∠BED=90°,
∴△AOB∽△DEB,
∴ ,
,
即 ,
,
∴BD= ,
,
∴S△BCD= BD•OC=
BD•OC= ×
× ×
× =
= .
.
点评:此题考查了相似三角形的判定与性质、点与一次函数的性质、勾股定理以及线段垂直平分线的性质.此题难度较大,注意掌握数形结合思想的应用.
 x+8,分别交x轴、y轴于A、B两点,即可求得点A与B的坐标,即可得OA,OB,由勾股定理即可求得AB的长,由CD是线段AB的垂直平分线,可求得AE与BE的长,易证得△AOB∽△AEC,然后由相似三角形的对应边成比例,即可求得AC的长,继而求得点C的坐标;
x+8,分别交x轴、y轴于A、B两点,即可求得点A与B的坐标,即可得OA,OB,由勾股定理即可求得AB的长,由CD是线段AB的垂直平分线,可求得AE与BE的长,易证得△AOB∽△AEC,然后由相似三角形的对应边成比例,即可求得AC的长,继而求得点C的坐标;(2)易证得△AOB∽△DEB,由相似三角形的对应边成比例,即可求得BD的长,又由S△BCD=
 BD•OC,即可求得△BCD的面积.
BD•OC,即可求得△BCD的面积.解答:解:(1)∵直线y=-
 x+8,分别交x轴、y轴于A、B两点,
x+8,分别交x轴、y轴于A、B两点,当x=0时,y=8;当y=0时,x=6.
∴OA=6,OB=8.
在Rt△AOB中,AB=
 =10,
=10,∵CD是线段AB的垂直平分线,
∴AE=BE=5.
∵∠OAB=∠CAE,∠AOB=∠AEC=90°,
∴△AOB∽△AEC,
∴
 ,
,即
 ,
,∴AC=
 .
.∴OC=AC-OA=
 ,
,∴点C的坐标为(-
 ,0);
,0);(2)∵∠ABO=∠DBE,∠AOB=∠BED=90°,
∴△AOB∽△DEB,
∴
 ,
,即
 ,
,∴BD=
 ,
,∴S△BCD=
 BD•OC=
BD•OC= ×
× ×
× =
= .
.点评:此题考查了相似三角形的判定与性质、点与一次函数的性质、勾股定理以及线段垂直平分线的性质.此题难度较大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 曲线
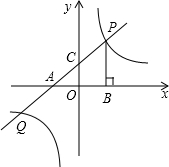
曲线 如图,直线l分别交x轴、y轴于A、B两点,且
如图,直线l分别交x轴、y轴于A、B两点,且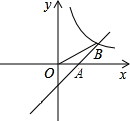 如图,直线y=x-1分别交x轴、反比例函数y=
如图,直线y=x-1分别交x轴、反比例函数y=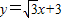 分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
 x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y=
x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y= 在第一象限内的交点,PB⊥x轴,垂足为点B,△APB的面积为4.
在第一象限内的交点,PB⊥x轴,垂足为点B,△APB的面积为4.