题目内容
14.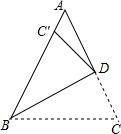 如图,在△ABC中,AB=AC,∠BAC=48°,点D在AC上,将△ABC沿BD折叠,若点C恰好落在AB边上的C′处,则∠AC′D的度数是114°.
如图,在△ABC中,AB=AC,∠BAC=48°,点D在AC上,将△ABC沿BD折叠,若点C恰好落在AB边上的C′处,则∠AC′D的度数是114°.
分析 先由等腰三角形的性质及三角形内角和定理求出∠C=66°,再由折叠的性质得出∠BC′D=∠C=66°,然后根据邻补角定义得到∠AC′D=114°.
解答 解:∵AB=AC,∠BAC=48°,
∴∠ABC=∠C=$\frac{1}{2}$(180°-48°)=66°.
∵将△BCD沿BD折叠,点C恰好落在AB边上的C′处,
∴∠BC′D=∠C=66°,
∴∠AC′D=180°-∠BC′D=114°.
故答案为114°.
点评 此题主要考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了等腰三角形的性质,三角形内角和定理以及邻补角定义.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
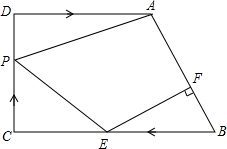 如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)
如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)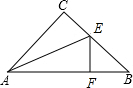 已知如图,∠C=90°,AE平分∠BAC交BC于E,EF⊥AB于F.
已知如图,∠C=90°,AE平分∠BAC交BC于E,EF⊥AB于F. 如图,观察图(1)中三棱柱有5个面,6个顶点,9条棱;四棱柱有6个面,8个顶点,12条棱;五棱柱有7个面,10个顶点,15条棱…由此推得
如图,观察图(1)中三棱柱有5个面,6个顶点,9条棱;四棱柱有6个面,8个顶点,12条棱;五棱柱有7个面,10个顶点,15条棱…由此推得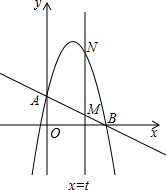 如图,一次函数y=-$\frac{1}{2}x+2$分别交y轴、x 轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.
如图,一次函数y=-$\frac{1}{2}x+2$分别交y轴、x 轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.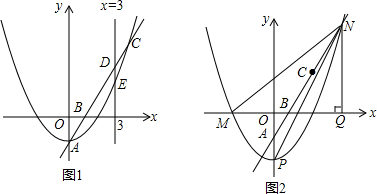
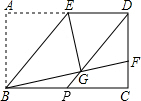 如图,矩形ABCD中,AB=6,BC=4$\sqrt{6}$,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.连接DG,并延长DG交BC于点P.
如图,矩形ABCD中,AB=6,BC=4$\sqrt{6}$,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.连接DG,并延长DG交BC于点P.