Question

如图，在梯形ABCD中，AD∥BC，AD=6cm，CD=4cm，BC=BD=10cm，点P由B出发沿BD方向匀速运动，速度为1cm/s；同时，线段EF由DC出发沿DA方向匀速运动，速度为1cm/s，交BD于Q，连接PE．时间为t（s）（0＜t＜5）．解答下列问题：
（1）求证：△DEQ∽△BCD；
（2）连接PF，在上述运动过程中，五边形PFCDE的面积是否发生变化？说明理由
（3）设△PEQ的面积为y（cm²），求y与t之间的函数关式．

Answer 1

分析：（1）利用AD∥BC可得出△EDQ∽△FBQ，再利用平移的性质得出EF∥CD，得出△FBQ∽△CBD，进而得出△DEQ∽△BCD；
（2）易得△PDE≌△FBP，故有S_{五边形PFCDE}=S_△PDE+S_{四边形PFCD=}S_△FBP+S_{四边形PFCD}=S_△BCD，即五边形的面积不变；
（3）过B作BM⊥CD，交CD于M，过P作PN⊥EF，交EF于N．由题意知，四边形CDEF是平行四边形，可证得△DEQ∽△BCD，得到

DE

BC

=

EQ

CD

，求得EQ的值，再由△PNQ∽△BMD，得到

PQ

BD

=

PN

BM

，求得PN的值，利用S_△PEQ=

1

2

EQ•PN得到y与t之间的函数关系式．

解答：（1）证明：∵AD∥BC，
∴△EDQ∽△FBQ，
∵线段EF由DC出发沿DA方向匀速运动，
∴EF∥CD，
∴△FBQ∽△CBD，
∴△DEQ∽△BCD；

（2）解：如图1，在△PDE和△FBP中，
∵DE=BP=t，PD=BF=10-t，∠PDE=∠FBP，
在△PDE和△FBP中，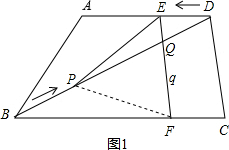

DE=PB ∠EDP=∠PBF DP=BF

，
∴△PDE≌△FBP（SAS）．
∴S_{五边形PFCDE}=S_△PDE+S_{四边形PFCD=}S_△FBP+S_{四边形PFCD}=S_△BCD=8

6

．
∴在运动过程中，五边形PFCDE的面积不变；

（3）解：如图2，
∵线段EF由DC出发沿DA方向匀速运动，
∴EF平行且等于CD，
∴四边形CDEF是平行四边形．
∴∠DEQ=∠C，∠DQE=∠BDC．
∵BC=BD=10，
∴△DEQ∽△BCD．
∴

DE

BC

=

EQ

CD

，
∴

t

10

=

EQ

4

．
∴EQ=

2

5

t．
过B作BM⊥CD，交CD于M，过P作PN⊥EF，交EF于N，
∵BC=BD，BM⊥CD，CD=4cm，
∴CM=

1

2

CD=2cm，
∴BM=

102-22

=4

6

（cm），
∵EF∥CD，
∴∠BQF=∠BDC，∠BFG=∠BCD，
又∵BD=BC，
∴∠BDC=∠BCD，
∴∠BQF=∠BFG，
∵ED∥BC，
∴∠DEQ=∠QFB，
又∵∠EQD=∠BQF，
∴∠DEQ=∠DQE，
∴DE=DQ，
∴ED=DQ=BP=t，
∴PQ=10-2t．
又∵△PNQ∽△BMD，
∴

PQ

BD

=

PN

BM

．
∴

10-2t

10

=

PN

4 6

．
∴PN=4

6

（1-

t

5

），
∴S_△PEQ=

1

2

EQ×PN=

1

2

×

2

5

t×4

6

（1-

t

5

）=-

4 6

25

t²+

4 6

5

t．

点评：本题考查了相似三角形和全等三角形的判定和性质，勾股定理，三角形的面积公式等知识，熟练利用相似三角形的性质表示出PN的长是解题关键．