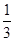题目内容
(1)观察图1,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2、…、G9,若∠BDC=140°,∠BG1C=77°,直接写出∠A的度数为

(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=
40°
40°
.②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2、…、G9,若∠BDC=140°,∠BG1C=77°,直接写出∠A的度数为
70°
70°
.
分析:(1)根据题意观察图形连接AD并延长至点F,由外角定理可知,一个三角形的外角等于与它不相邻的两个内角的和,则容易得到∠BDC=∠BDF+∠CDF;
(2)①由(1)的结论可得∠ABX+∠ACX+∠A=∠BXC,然后把∠A=50°,∠BXC=90°代入上式即可得到∠ABX+∠ACX的值.
②结合图形可得∠DBE=∠DAE+∠ADB+∠AEB,代入∠DAE=50°,∠DBE=130°即可得到∠ADB+∠AEB的值,再利用上面得出的结论可知∠DCE=
(∠ADB+∠AEB)+∠A,易得答案.
③由(2)的方法,进而可得答案.
(2)①由(1)的结论可得∠ABX+∠ACX+∠A=∠BXC,然后把∠A=50°,∠BXC=90°代入上式即可得到∠ABX+∠ACX的值.
②结合图形可得∠DBE=∠DAE+∠ADB+∠AEB,代入∠DAE=50°,∠DBE=130°即可得到∠ADB+∠AEB的值,再利用上面得出的结论可知∠DCE=
| 1 |
| 2 |
③由(2)的方法,进而可得答案.
解答: 解:(1)∠BDC=∠A+∠B+∠C.
解:(1)∠BDC=∠A+∠B+∠C.
理由如下:
连接AD并延长到E点
∵∠BDE=∠BAE+∠B
∠EDC=∠EAC+∠C
∴∠BDE+∠EDC=∠BAE+∠EAC+∠B+∠C
∵∠BDC=∠BDE+∠EDC
∠BAC=∠BAE+∠EAC
∴∠BDC=∠BAC+∠B+∠C
(2)①由(1)的结论易得:∠ABX+∠ACX+∠A=∠BXC,
又因为∠A=50°,∠BXC=90°,
所以∠ABX+∠ACX=90°-50°=40°;
故答案是:40°;
②由(1)的结论易得∠DBE=∠A+∠ADB+∠AEB,易得∠ADB+∠AEB=80°;
而∠DCE=
(∠ADB+∠AEB)+∠A,
代入∠DAE=50°,∠DBE=130°,易得∠DCE=90°;
③如图4,∠BG1C=
(∠ABD+∠ACD)+∠A,
∵∠BG1C=77°,
∴设∠A为x°,
∵∠ABD+∠ACD=140°-x°
∴
(140-x)+x=77,
14-
x+x=77,
x=70
∴∠A为70°.
故答案是:70°.
 解:(1)∠BDC=∠A+∠B+∠C.
解:(1)∠BDC=∠A+∠B+∠C.理由如下:
连接AD并延长到E点
∵∠BDE=∠BAE+∠B
∠EDC=∠EAC+∠C
∴∠BDE+∠EDC=∠BAE+∠EAC+∠B+∠C
∵∠BDC=∠BDE+∠EDC
∠BAC=∠BAE+∠EAC
∴∠BDC=∠BAC+∠B+∠C
(2)①由(1)的结论易得:∠ABX+∠ACX+∠A=∠BXC,
又因为∠A=50°,∠BXC=90°,
所以∠ABX+∠ACX=90°-50°=40°;
故答案是:40°;
②由(1)的结论易得∠DBE=∠A+∠ADB+∠AEB,易得∠ADB+∠AEB=80°;
而∠DCE=
| 1 |
| 2 |
代入∠DAE=50°,∠DBE=130°,易得∠DCE=90°;
③如图4,∠BG1C=
| 1 |
| 10 |
∵∠BG1C=77°,
∴设∠A为x°,
∵∠ABD+∠ACD=140°-x°
∴
| 1 |
| 10 |
14-
| 1 |
| 10 |
x=70
∴∠A为70°.
故答案是:70°.
点评:本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本题10分)问题情境
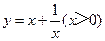
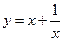
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
①填写下表,画出函数的图象:
②观察图象,试描述该函数的增减性(y随x变化发生什么变化);③在求二次函数y=ax+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过
配方得到.请你通过配方求函数(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
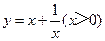
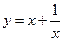
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
①填写下表,画出函数的图象:
| x | …… | 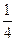 | 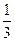 | 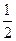 | 1 | 2 | 3 | 4 | …… |
| y | …… | | | | | | | | …… |

|
配方得到.请你通过配方求函数(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
(本题10分)问题情境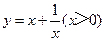

已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
①填写下表,画出函数的图象:
| x | …… |  | 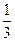 | 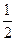 | 1 | 2 | 3 | 4 | …… |
| y | …… | | | | | | | | …… |
|
配方得到.请你通过配方求函数(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
(本题10分)问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
 探索研究
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
①填写下表,画出函数的图象:
|
x |
…… |
|
|
|
1 |
2 |
3 |
4 |
…… |
|
y |
…… |
|
|
|
|
|
|
|
…… |

|
③在求二次函数y=ax+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过
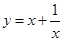
配方得到.请你通过配方求函数(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.