题目内容
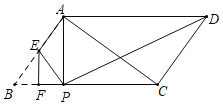
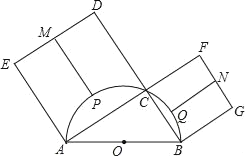
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=![]() ,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A.P是弧AB上的一个动点.
,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A.P是弧AB上的一个动点.
(1)求半径OB的长;
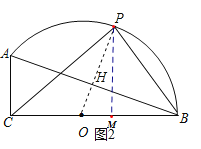
(2)如果点P是弧AB的中点,联结PC,求∠PCB的正切值;
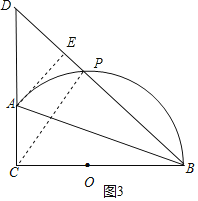
(3)如果BA平分∠PBC,延长BP、CA交于点D,求线段DP的长.
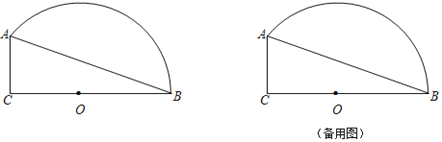
【答案】(1)OB=9;(2)∠PCB的正切值=![]() (3)PD=
(3)PD=![]() .
.
【解析】
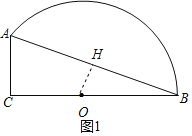
(1)根据勾股定理得到AB=![]() =12
=12![]() ,如图1,过O作OH⊥AB于H,根据相似三角形的性质即可得到结论;
,如图1,过O作OH⊥AB于H,根据相似三角形的性质即可得到结论;
(2)如图2,连接OP交AB于H,根据垂径定理得到OP⊥AB,AH=BH=![]() AB=6
AB=6![]() ,根据勾股定理得到OH=3,过P作PM⊥OB于M,证明△OBH≌△OPM ,得到
,根据勾股定理得到OH=3,过P作PM⊥OB于M,证明△OBH≌△OPM ,得到![]()
![]()
![]()
![]() 根据三角函数的定义即可得到结论;
根据三角函数的定义即可得到结论;
(3)如图3,过A作AE⊥BD于E,连接CP,根据角平分线的性质得到AE=AC=4![]() ,根据相似三角形的性质得到AD=
,根据相似三角形的性质得到AD=![]() ,根据全等三角形的性质得到BE=BC=16,根据勾股定理和三角形的面积公式即可得到结论.
,根据全等三角形的性质得到BE=BC=16,根据勾股定理和三角形的面积公式即可得到结论.
解:(1)∵Rt△ABC中,∠ACB=90°,AC=![]() ,BC=16,
,BC=16,
∴AB=![]() =12
=12![]() ,
,
如图1,过O作OH⊥AB于H,
则BH=![]() AB=6
AB=6![]() ,
,
∵∠BHO=∠ACB=90°,∠B=∠B,
∴△BHO∽△BCA,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴OB=9;
(2)如图2,连接OP交AB于H,
∵点P是弧AB的中点,
∴OP⊥AB,AH=BH=![]() AB=6
AB=6![]() ,
,
在Rt△BHO中,OH=![]() =
=![]() =3,
=3,
过P作PM⊥OB于M,
在△OBH与△OPM中,
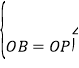
∴△OBH≌△△OPM (AAS),
![]()
![]()
![]()
![]()
∴∠PCB的正切值![]()
(3)如图3,过A作AE⊥BD于E,连接CP,
∵BA平分∠PBC,AC⊥BC,
∴AE=AC=4![]() ,
,
∵∠AED=∠ACB=90°,∠D=∠D,
∴△ADE∽△BDC,
∴![]() =
=![]() ,
,
设DE=x,
∴![]() =
=![]() ,
,
∴AD=![]() ,
,
在Rt△ACB与Rt△AEB中,![]() ,
,
∴Rt△ACB≌Rt△AEB(HL),
∴BE=BC=16,
∵CD2+BC2=BD2,
∴(4![]() +
+![]() )2+162=(16+x)2,
)2+162=(16+x)2,
解得:x=![]() ,
,
∴AD=![]() ,BD=16+
,BD=16+![]() =
=![]() ,
,
∴CD=![]() ,
,
∵BC是⊙的直径,
∴CP⊥BD,
∴CP=![]() =
=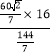 =
=![]() ,
,
∴PD=![]() =
=![]() .
.