题目内容
已知两函数:反比例函数 和二次函数y=
和二次函数y= x2+x+a.
x2+x+a.
(1)若两个函数的图象都经过点(2,2).
①求两函数的表达式;
②证明反比例函数的图象经过二次函数图象的顶点.
(2)若二次函数y= x2+x+a的图象与x轴有两个不同的交点,是否存在实数a,使方程
x2+x+a的图象与x轴有两个不同的交点,是否存在实数a,使方程 x2+x+a=0的两个实数根的倒数和等于-1?若存在,求出a的值;若不存在,说明理由.
x2+x+a=0的两个实数根的倒数和等于-1?若存在,求出a的值;若不存在,说明理由.
(1)①解:根据题意,把x=2,y=2分别代入两个函数的表达式,
由2= 得k=4,
得k=4,
所以反比例函数为 ,
,
由2=1+2+a得a=-1,
所以二次函数为y= x2+x-1,
x2+x-1,
答:两函数的表达式分别是 ,y=
,y= x2+x-1.
x2+x-1.
②证明:由y= x2+x-1=
x2+x-1= 知,
知,
二次函数图象的顶点坐标为(-2,-2),
又当x=-2时,y= ,
,
所以反比例函数的图象经过二次函数图象的顶点.
(2)解:不存在符合条件的a的值,
理由:根据题意,由△=1-4× a>0得a<1,
a>0得a<1,
∴a的取值范围是a<1,
设方程 x2+x+a=0的两根分别为x1、x2,
x2+x+a=0的两根分别为x1、x2,
由根与系数关系有:
x1+x2=-4,x1•x2=4a,
又 ,
,
由 ,
,
得a=1这与a<1不符,
∴不存在符合条件的a的值.
答:不存在
分析:(1)①把x=2,y=2分别代入两个函数的表达式,就能求出k和a的值,即可得到两函数的表达式;②先求出二次函数图象的顶点坐标,把顶点坐标代入反比例函数的解析式,看两边是否相等即可;
(2)不存在符合条件的a的值,理由是先根据根的判别式求出a的范围,设方程 x2+x+a=0的两根分别为x1、x2,根据根与系数关系有:x1+x2=-4,x1•x2=4a,求出
x2+x+a=0的两根分别为x1、x2,根据根与系数关系有:x1+x2=-4,x1•x2=4a,求出 +
+ 的值即可求出a=1,与求出的a的取值范围a<1不符,即可判断答案.
的值即可求出a=1,与求出的a的取值范围a<1不符,即可判断答案.
点评:本题主要考查对二次函数的性质,解一元一次方程,根的判别式,根与系数的关系,用待定系数法求反比例函数、二次函数的解析式等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键,题型较好,综合性强.
由2=
 得k=4,
得k=4,所以反比例函数为
 ,
,由2=1+2+a得a=-1,
所以二次函数为y=
 x2+x-1,
x2+x-1,答:两函数的表达式分别是
 ,y=
,y= x2+x-1.
x2+x-1.②证明:由y=
 x2+x-1=
x2+x-1= 知,
知,二次函数图象的顶点坐标为(-2,-2),
又当x=-2时,y=
 ,
,所以反比例函数的图象经过二次函数图象的顶点.
(2)解:不存在符合条件的a的值,
理由:根据题意,由△=1-4×
 a>0得a<1,
a>0得a<1,∴a的取值范围是a<1,
设方程
 x2+x+a=0的两根分别为x1、x2,
x2+x+a=0的两根分别为x1、x2,由根与系数关系有:
x1+x2=-4,x1•x2=4a,
又
 ,
,由
 ,
,得a=1这与a<1不符,
∴不存在符合条件的a的值.
答:不存在
分析:(1)①把x=2,y=2分别代入两个函数的表达式,就能求出k和a的值,即可得到两函数的表达式;②先求出二次函数图象的顶点坐标,把顶点坐标代入反比例函数的解析式,看两边是否相等即可;
(2)不存在符合条件的a的值,理由是先根据根的判别式求出a的范围,设方程
 x2+x+a=0的两根分别为x1、x2,根据根与系数关系有:x1+x2=-4,x1•x2=4a,求出
x2+x+a=0的两根分别为x1、x2,根据根与系数关系有:x1+x2=-4,x1•x2=4a,求出 +
+ 的值即可求出a=1,与求出的a的取值范围a<1不符,即可判断答案.
的值即可求出a=1,与求出的a的取值范围a<1不符,即可判断答案.点评:本题主要考查对二次函数的性质,解一元一次方程,根的判别式,根与系数的关系,用待定系数法求反比例函数、二次函数的解析式等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键,题型较好,综合性强.

练习册系列答案
相关题目
 (2013•佛山)已知正比例函数y=ax与反比例函数
(2013•佛山)已知正比例函数y=ax与反比例函数 已知正比例函数y=ax与反比例函数
已知正比例函数y=ax与反比例函数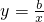 的图象有一个公共点A(1,2).
的图象有一个公共点A(1,2).
 已知正比例函数y=ax与反比例函数
已知正比例函数y=ax与反比例函数 的图象有一个公共点A(1,2).
的图象有一个公共点A(1,2). 的图象有一个公共点A(1,2).
的图象有一个公共点A(1,2).