Question

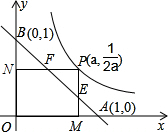如图，P是函数y=

1

2x

（x＞0）图象上一点，直线y=-x+1分别交x轴、y轴于点A、B，作PM⊥x轴于点M，交AB于点E，作PN⊥y轴于点N，交AB于点F．则AF•BE的值为（　　）

• A、2
• B、

  2

• C、1
• D、

  1

  2

Answer 1

分析：由于P的坐标为（a，

1

2a

），且PN⊥OB，PM⊥OA，那么N的坐标和M点的坐标都可以a表示，那么BN、NF的长度也可以用a表示，接着F点、E点的坐标也可以a表示，然后利用勾股定理可以分别用a表示AF，BE，最后即可求出AF•BE．

解答：解：∵P的坐标为（a，

1

2a

），且PN⊥OB，PM⊥OA，
∴N的坐标为（0，

1

2a

），M点的坐标为（a，0），
∴BN=1-

1

2a

，
在直角三角形BNF中，∠NBF=45°（OB=OA=1，三角形OAB是等腰直角三角形），
∴NF=BN=1-

1

2a

，
∴F点的坐标为（1-

1

2a

，

1

2a

），
同理可得出E点的坐标为（a，1-a），
∴AF²=（-

1

2a

）²+（

1

2a

）²=

1

2a2

，BE²=（a）²+（-a）²=2a²，
∴AF²•BE²=

1

2a2

•2a²=1，即AF•BE=1．
故选C．

点评：本题考查了反比例函数的知识，解题关键是通过反比例函数上的点P来确定E、F两点的坐标，进而通过坐标系中两点的距离公式得出所求的值．