Question

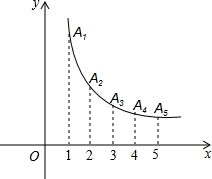已知：反比例函数y=

m

x

(m＞0)的图象在第一象限的分支上有n个点A₁（1，y₁），A₂（2，y₂），…，A_n（n，y_n），设直线A₁A₂的解析式为y=k₁x+b₁，A₂A₃的解析式为y=k₂x+b₂，…，A_nA_n+1的解析式为y=k_nx+b_n．
（1）当m=1时，k₁=

-

1

2

；
（2）当m=1时，k₁+k₂+k₃=

-

3

4

；
（3）①当m=2时，求k₁+k₂+k₃+…+k₂₀的值，并写出求解过程．
     ②用m、n表示k₁+k₂+k₃+…+k_n的值（直接写出结果）．

Answer 1

分析：（1）由反比例函数的解析式y=

1

x

可确定点A₁的坐标为（1，1），点A₂的坐标为（2，

1

2

），再把它们代入y=k₁x+b₁得到k₁+b₁=1①，2k₁x+b₁=

1

2

②，然后用②-①可求得k₁=

1

2

-1=-

1

2

；
（2）当m=1时，反比例函数的解析式为y=

1

x

，可确定点A₁的坐标为（1，1），点A₂的坐标为（2，

1

2

），点A₃的坐标为（3，

1

3

），点A₄的坐标为（4，

1

4

），与（1）一样得到k₂=

1

3

-

1

2

，k₃=

1

4

-

1

3

，易得到k₁+k₂+k₃的值；
（3）①当m=2时，反比例函数的解析式为y=

2

x

，先确定点A₁坐标为（1，2），点A₂坐标为（2，

2

2

），点A₃的坐标为（3，

2

3

），点A₄的坐标为（4，

2

4

），…，点A₂₀坐标为（20，

2

20

），点A₂₁坐标为（21，

2

21

），仿照（1）得到k₁=

2

2

-

2

1

，k₂=

2

3

-

2

2

，k₃=

2

4

-

2

3

，…，k₂₀=

2

21

-

2

20

，则k₁+k₂+k₃+…+k₂₀=

2

2

-

2

1

+

2

3

-

2

2

+

2

4

-

2

3

+…+

2

21

-

2

20

，然后进行加减运算即可；
②先得到点A₁坐标为（1，m），点A₂坐标为（2，

m

2

），点A₃的坐标为（3，

m

3

），点A₄的坐标为（4，

m

4

），…，点A_n坐标为（n，

m

n

），点A_n+1坐标为（n+1，

m

n+1

），再同样可得到k₁=

m

2

-m，k₂=

m

3

-

m

2

，k₃=

m

4

-

m

3

，…，k_n=

m

n+1

-

m

n

，则k₁+k₂+k₃+…+k_n=

m

2

-m+

m

3

-

m

2

+

m

4

-

m

3

+…+

m

n+1

-

m

n

，然后进行分式的加减运算即可．

解答：解：（1）当m=1时，反比例函数的解析式为y=

1

x

，
∴点A₁的坐标为（1，1），点A₂的坐标为（2，

1

2

），
把点A₁（1，1），点A₂（2，

1

2

）代入y=k₁x+b₁得
k₁+b₁=1①，
2k₁x+b₁=

1

2

②
∴②-①得k₁=

1

2

-1=-

1

2

；
故答案为-

1

2

；

（2）当m=1时，反比例函数的解析式为y=

1

x

，
点A₁的坐标为（1，1），点A₂的坐标为（2，

1

2

），点A₃的坐标为（3，

1

3

），点A₄的坐标为（4，

1

4

），
与（1）一样，k₂=

1

3

-

1

2

，k₃=

1

4

-

1

3

，
∴k₁+k₂+k₃=

1

2

-1+

1

3

-

1

2

+

1

4

-

1

3

=-1+

1

4

=-

3

4

；
故答案为-

3

4

；

（3）①当m=2时，反比例函数的解析式为y=

2

x

，
∴点A₁坐标为（1，2），点A₂坐标为（2，

2

2

），点A₃的坐标为（3，

2

3

），点A₄的坐标为（4，

2

4

），…，点A₂₀坐标为（20，

2

20

），点A₂₁坐标为（21，

2

21

），
与（1）一样，k₁=

2

2

-

2

1

，k₂=

2

3

-

2

2

，k₃=

2

4

-

2

3

，…，k₂₀=

2

21

-

2

20

，
∴k₁+k₂+k₃+…+k₂₀=

2

2

-

2

1

+

2

3

-

2

2

+

2

4

-

2

3

+…+

2

21

-

2

20

=-2+

2

21

=-

40

21

；
②点A₁坐标为（1，m），点A₂坐标为（2，

m

2

），点A₃的坐标为（3，

m

3

），点A₄的坐标为（4，

m

4

），…，点A_n坐标为（n，

m

n

），点A_n+1坐标为（n+1，

m

n+1

）．
与（1）一样，k₁=

m

2

-m，k₂=

m

3

-

m

2

，k₃=

m

4

-

m

3

，…，k_n=

m

n+1

-

m

n

，
∴k₁+k₂+k₃+…+k_n=

m

2

-m+

m

3

-

m

2

+

m

4

-

m

3

+…+

m

n+1

-

m

n

=-m+

m

n+1

=-

mn

n+1

．

点评：本题考查了反比例函数综合题：点在反比例函数图象上，则点的坐标满足其解析式；运用待定系数法求函数的解析式；熟练掌握分数与分式的运算．