Question

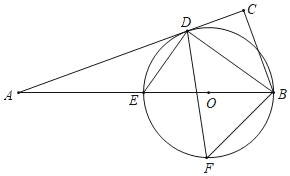
【题目】如图，在△ABC中，∠C＝90°，点O为BE上一点，以OB为半径的⊙O交AB于点E，交AC于点D．BD平分∠ABC．

（1）求证：AC为⊙O切线；

（2）点F为的中点，连接BF，若BC＝，BD＝8，求⊙O半径及DF的长．

Answer 1

【答案】（1）证明见解析（2）7

【解析】

（1）连接OD，根据角平分线的性质得到∠CBD＝∠OBD，根据角平分线的定义得到∠ODB＝∠OBD，推出OD∥BC，得到∠ADO＝∠C＝90°，于是得到结论；

（2）由BE为⊙O的直径，得到∠BDE＝90°，根据相似三角形的性质得到BE＝10，求得⊙O半径OB＝5；推出∠EDF＝∠BDF＝45°，过B作BM⊥DF于M，过E作EN⊥DF于N，连接EF，解直角三角形得到BM＝BD＝4，EN＝DE＝3，EF＝BE＝5，根据三角形的面积公式列方程即可得到结论．

（1）证明：连接OD，

∵BD平分∠ABC，

∴∠CBD＝∠OBD，

∵OB＝OD，

∴∠ODB＝∠OBD，

∴∠ODB＝∠CBD，

∴OD∥BC，

∴∠ADO＝∠C＝90°，

∴OD⊥AC，

∴AC为⊙O切线；

（2）解：∵BE为⊙O的直径，

∴∠BDE＝90°，

∴∠C＝∠BDE，

∵∠CBD＝∠EBD，

∴△CBD∽△DBE，

∴，

即，

∴BE＝10，

∴⊙O半径OB＝5；

∴DE＝6，

∵点F为的中点，

∴，

∴∠EDF＝∠BDF＝45°，

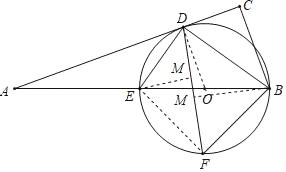
过B作BM⊥DF于M，过E作EN⊥DF于N，连接EF，

∴BM＝BD＝4，EN＝DE＝3，EF＝BE＝5，

∴S四边形BDEF＝S△BEF+S△BDE＝S△DEF+S△DBF，

∴×5×5+×6×8＝×3DF+×4DF，

∴DF＝7．