Question

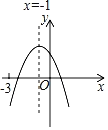
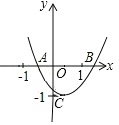
【题目】抛物线y＝x2+bx+c的对称轴为直线x＝1，且经过点（﹣1，0）．若关于x的一元二次方程x2+bx+c﹣t＝0（t为实数）在﹣1＜x＜4的范围内有实数根，则t的取值范围是________．

Answer 1

【答案】

【解析】

先根据二次函数对称轴公式得出b的值，将代入二次函数解析式得出的值，再根据二次函数的性质得出在中，y的取值范围，最后根据一元二次方程有实数根得出与的图像在中有交点即得．

∵抛物线的对称轴为直线x＝1

∴，解得：

∵抛物线经过点

∴，解得：

∴抛物线的解析式是

∵

∴当时，

∵当时，

当时，

∴在抛物线中，当时，

∴令，要使与有交点，则

∵关于x的一元二次方程（t为实数）在﹣1＜x＜4的范围内有实数根

∴与的图像在中有交点

∴

故答案为：