题目内容
3.若关于x的方程$\frac{k}{x-2}$+$\frac{x}{2-x}$=3有增根,则k的值为2.分析 先把分式方程化为整式方程解得x=$\frac{k+6}{4}$,由于原方程的增根只能为2,于是把x=2代入x=$\frac{k+6}{4}$中求出对应的k的值即可.
解答 解:去分母得k-x=3(x-2),
解得x=$\frac{k+6}{4}$,
当x=2时,$\frac{k+6}{4}$=2,解得k=2,
即当k=2时,关于x的方程$\frac{k}{x-2}$+$\frac{x}{2-x}$=3有增根.
故答案为2.
点评 本题考查了分式方程的增根:把由分式方程化成的整式方程的解代入最简公分母,看最简公分母是否为0,如果为0,则是增根;如果不是0,则是原分式方程的根.

练习册系列答案
相关题目
11.下面式子从左边到右边的变形是因式分解的是( )
| A. | x2-x-2=x(x-1)-2 | B. | x2-4x+4=(x-2)2 | C. | (x+1)(x-1)=x2-1 | D. | x-1=x(1-$\frac{1}{x}$) |
13.下列实数中,有理数是( )
| A. | π | B. | $\root{3}{4}$ | C. | 2$\sqrt{5}$ | D. | $\frac{7}{11}$ |
 如图,四边形ABCD是菱形,如果AB=5,那么菱形ABCD的周长是20.
如图,四边形ABCD是菱形,如果AB=5,那么菱形ABCD的周长是20.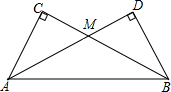 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,MC=4cm,则点M到直线AB的距离为4cm.
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,MC=4cm,则点M到直线AB的距离为4cm.