题目内容
 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为考点:直角三角形斜边上的中线,等腰三角形的判定与性质,含30度角的直角三角形
专题:
分析:过点D作DE⊥AB于E,根据直角三角形两锐角互余求出∠A=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求出DE,根据角平分线上的点到角的两边距离相等可得CD=DE,根据角平分线的定义求出∠CBD=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出BD,再根据直角三角形斜边上的中线等于斜边的一半求解.
解答: 解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,
∵∠ACB=90°,∠ABC=60°,
∴∠A=90°-60°=30°,
∴DE=
AD=
×6=3,
又∵BD平分∠ABC,
∴CD=DE=3,
∵∠ABC=60°,BD平分∠ABC,
∴∠CBD=30°,
∴BD=2CD=2×3=6,
∵P点是BD的中点,
∴CP=
BD=
×6=3.
故答案为:3.
 解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,∵∠ACB=90°,∠ABC=60°,
∴∠A=90°-60°=30°,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
又∵BD平分∠ABC,
∴CD=DE=3,
∵∠ABC=60°,BD平分∠ABC,
∴∠CBD=30°,
∴BD=2CD=2×3=6,
∵P点是BD的中点,
∴CP=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:3.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半,角平分线上的点到角的两边距离相等的性质,熟记各性质并作出辅助线是解题的关键.

练习册系列答案
相关题目
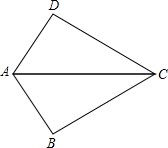 如图,已知AB=AD,那么添加下列一个条件后,能用SAS判定△ABC≌△ADC的是
如图,已知AB=AD,那么添加下列一个条件后,能用SAS判定△ABC≌△ADC的是