题目内容
理解与思考:
(1)求出下列每对数在数轴上的对应点间的距离:
①3与-2在数轴上对应点间的距离是 ,②-7与-3在数轴上对应点间的距离是 ,
③4与6在数轴上对应点间的距离是 ,④-3与2在数轴上对应点间的距离是 .
(2)若数轴上的点A表示的数为x,点B表示的数为-1,则A与B两点间的距离可以表示为 .
(3)结合数轴直接写出|x-3|+|x+2|的最小值,并写出取得最小值时x的取值范围.
(1)求出下列每对数在数轴上的对应点间的距离:
①3与-2在数轴上对应点间的距离是
③4与6在数轴上对应点间的距离是
(2)若数轴上的点A表示的数为x,点B表示的数为-1,则A与B两点间的距离可以表示为
(3)结合数轴直接写出|x-3|+|x+2|的最小值,并写出取得最小值时x的取值范围.
考点:数轴,绝对值
专题:
分析:(1)利用数轴分别得出,进而得出两数所对应的两点之间的距离;
(2)结合数轴,我们发现应分以下三种情况进行讨论.

当x<-1时,距离为-x-1,

当-1<x<0时,距离为x+1,

当x>0,距离为x+1.综上,我们得到A与B两点间的距离可以表示为|x+1|;
(3)为x为有理数,所以要分类讨论x-3与x+2的正负,再去掉绝对值符号再计算.
(2)结合数轴,我们发现应分以下三种情况进行讨论.

当x<-1时,距离为-x-1,

当-1<x<0时,距离为x+1,

当x>0,距离为x+1.综上,我们得到A与B两点间的距离可以表示为|x+1|;
(3)为x为有理数,所以要分类讨论x-3与x+2的正负,再去掉绝对值符号再计算.
解答:解:(1)直接借助数轴可以得出:
①3与-2在数轴上对应点间的距离是5,②-7与-3在数轴上对应点间的距离是4,
③4与6在数轴上对应点间的距离是2,④-3与2在数轴上对应点间的距离是5.
(2)当x<-1时,距离为-x-1,
当-1<x<0时,距离为x+1,
当x>0,距离为x+1.综上,我们得到A与B两点间的距离可以表示为|x+1|;
(3)因为x为有理数,就是说x可以为正数,也可以为负数,也可以为0,所以要分情况讨论.
①当x<-2时,x-3<0,x+2<0,所以|x-3|+|x+2|=-(x-3)-(x+2)=-2x+1>5;
②当-2≤x<3时,x-3<0,x+2≥0,所以|x-3|+|x+2|=-(x-3)+(x+2)=5;
③当x≥3时,x-3≥0,x+2>0,所以|x-3|+|x+2|=(x-3)+(x+2)=2x-1≥5;
综上所述,|x-3|+|x+2|的最小值是5,取值范围为-2和3之间(-2≤x≤3).
故答案为:5,4,2,5;
|x+1|或|-1-x|;
5,-2和3之间(-2≤x≤3).
①3与-2在数轴上对应点间的距离是5,②-7与-3在数轴上对应点间的距离是4,
③4与6在数轴上对应点间的距离是2,④-3与2在数轴上对应点间的距离是5.
(2)当x<-1时,距离为-x-1,
当-1<x<0时,距离为x+1,
当x>0,距离为x+1.综上,我们得到A与B两点间的距离可以表示为|x+1|;
(3)因为x为有理数,就是说x可以为正数,也可以为负数,也可以为0,所以要分情况讨论.
①当x<-2时,x-3<0,x+2<0,所以|x-3|+|x+2|=-(x-3)-(x+2)=-2x+1>5;
②当-2≤x<3时,x-3<0,x+2≥0,所以|x-3|+|x+2|=-(x-3)+(x+2)=5;
③当x≥3时,x-3≥0,x+2>0,所以|x-3|+|x+2|=(x-3)+(x+2)=2x-1≥5;
综上所述,|x-3|+|x+2|的最小值是5,取值范围为-2和3之间(-2≤x≤3).
故答案为:5,4,2,5;
|x+1|或|-1-x|;
5,-2和3之间(-2≤x≤3).
点评:本题考查了数轴,借助数轴可以使有关绝对值的问题转化为数轴上有关距离的问题,反之,有关数轴上的距离问题也可以转化为绝对值问题.这种相互转化在解决某些问题时可以带来方便.事实上,|A-B|表示的几何意义就是在数轴上表示数A与数B的点之间的距离.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )作法:
①以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E;
②分别以D,E为圆心,大于DE的长为半径画弧,两弧在∠AOB内交于一点C;
③画射线OC,射线OC就是∠AOB的角平分线.
| A、ASA | B、SAS |
| C、SSS | D、AAS |
 如图,OP平分∠BOA,∠BOA=30°,PC∥OA,若PC=4,则点P到OA的距离( )
如图,OP平分∠BOA,∠BOA=30°,PC∥OA,若PC=4,则点P到OA的距离( )| A、4 | ||
B、2
| ||
C、2
| ||
| D、2 |
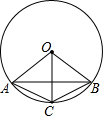 如图,AB、AC、BC都是⊙O的弦,∠AOC=∠BOC.
如图,AB、AC、BC都是⊙O的弦,∠AOC=∠BOC. 若在△ABC中,D是AB的中点,且DE∥BC,求证:DE是△ABC的中位线.
若在△ABC中,D是AB的中点,且DE∥BC,求证:DE是△ABC的中位线.