题目内容
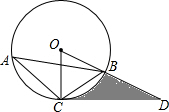 如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°,
如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°,(1)试判断直线CD与⊙O的位置关系,并说明理由.
(2)若CD长为
| 3 |
分析:(1)由已知可证得OC⊥CD,OC为圆的半径所以直线CD与⊙O相切;
(2)根据已知可求得OC,CD的长,则利用S阴影=S△COD-S扇形OCB求得阴影部分的面积.
(2)根据已知可求得OC,CD的长,则利用S阴影=S△COD-S扇形OCB求得阴影部分的面积.
解答:解:(1)直线CD与⊙O相切,
∵在⊙O中,∠COB=2∠CAB=2×30°=60°,
又∵OB=OC,
∴△OBC是正三角形,
∴∠OCB=60°,
又∵∠BCD=30°,
∴∠OCD=60°+30°=90°,
∴OC⊥CD,
又∵OC是半径,
∴直线CD与⊙O相切.
(2)∵∠OCD=90°,∠O=60°,
∴∠D=30°,
∵CD=
,
∴CO=CD•tanD=1,
∴S△COD=
OC•CD=
,
又∵S扇形OCB=
=
,
∴S阴影=S△COD-S扇形OCB=
-
=
.
∵在⊙O中,∠COB=2∠CAB=2×30°=60°,
又∵OB=OC,
∴△OBC是正三角形,

∴∠OCB=60°,
又∵∠BCD=30°,
∴∠OCD=60°+30°=90°,
∴OC⊥CD,
又∵OC是半径,
∴直线CD与⊙O相切.
(2)∵∠OCD=90°,∠O=60°,
∴∠D=30°,
∵CD=
| 3 |
∴CO=CD•tanD=1,
∴S△COD=
| 1 |
| 2 |
| ||
| 2 |
又∵S扇形OCB=
| 60π×12 |
| 360 |
| π |
| 6 |
∴S阴影=S△COD-S扇形OCB=
| ||
| 2 |
| π |
| 6 |
3
| ||
| 6 |
点评:此题主要考查了对切线的性质及扇形的面积公式,关键是掌握切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线,以及扇形的面积计算公式.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD=
15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD= 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.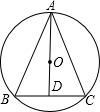 已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积.
已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积. 18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )
18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( ) 如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.
如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.