题目内容
如图，四边形ABCD内接于⊙O，∠BOD=70°，则∠BCD的度数是（ ）| A、70° | B、100° |
| C、145° | D、150° |
考点：圆内接四边形的性质,圆周角定理
专题：
分析：先根据圆周角定理求出∠A的度数，再由圆内接四边形的性质即可得出结论．
解答：解：∵∠A与∠BOD是同弧所对的圆周角与圆心角，∠BOD=70°，
∴∠A=
∠BOD=35°．
∵四边形ABCD是圆内接四边形，
∴∠BCD=180°-∠A=180°-35°=145°．
故选C．
∴∠A=
| 1 |
| 2 |
∵四边形ABCD是圆内接四边形，
∴∠BCD=180°-∠A=180°-35°=145°．
故选C．
点评：本题考查的是圆内接四边形的性质，熟知圆内接四边形的对角互补是解答此题的关键．
练习册系列答案
相关题目
下列解方程变形正确的是（ ）
| A、由2x-1=3得2x=3-1 | ||||
B、由-75x=76得x=
| ||||
| C、由2x=-3得x=3 | ||||
D、由
|
如图所示，△ABC三个顶点A，B，C的坐标分别为A（1，2），B（4，3），C（3，1），把△A1B1C1向右平移4个单位，再向下平移3个单位，恰好得到△ABC，试写出△A1B1C1三个顶点．
如图的坐标平面上有四条直线l1、l2、l3、l4，则方程3x-5y+15=0表示那一条直线？（ ）| A、l1 |
| B、l2 |
| C、l3 |
| D、l4 |
如图，数轴上点P表示的数可能是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
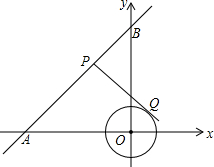如图，在平面直角坐标系xOy中，直线AB过点A（-3
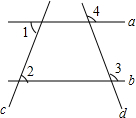如图，已知：∠1=∠2，∠3=110°，求∠4的度数．