题目内容
3. 如图,在平面直角坐标系中,直线AB:y1=x+m与双曲线C;y2=$\frac{k}{x}$相交于A、B两点,其中A点(2,5),AC⊥y轴于C.
如图,在平面直角坐标系中,直线AB:y1=x+m与双曲线C;y2=$\frac{k}{x}$相交于A、B两点,其中A点(2,5),AC⊥y轴于C.(1)求直线与双曲线的解析式;
(2)直接写出x<2时.反比例函数值y2的取值范围;
(3)点E为B点下方直线AB上一动点,直线EF⊥AB,
分别与直线AB、双曲线C、y轴交于E、F、G三点,求EF•FG的最大值.
分析 (1)由A点坐标,利用待定系数法可坟得直线AB和双曲线C的解析式;
(2)结合图象可知反比例函数图象应该在A点的左侧,则可求得其函数值的取值范围;
(3)过E作EM⊥y轴于点M,过F作FN⊥y轴于点N,过F作FP⊥EM于点P,由AB的解析式可求得∠EGM=∠EFP=∠MEG=45°,可设E(t,t+3),F(s,$\frac{10}{s}$),利用等腰直角三角形的性质可得到t、s之间的关系,再利用s表示出EF•FG,利用二次函数的性质可求得其最大值.
解答 解:
(1)∵A(2,5)为两函数图象的交点,
∴5=2+m,5=$\frac{k}{2}$,解得m=3,k=10,
∴直线解析式为y=x+3,双曲线解析式为y=$\frac{10}{x}$;
(2)∵A(2,5),
∴当x<2时,即反比例函数图象在A点的左侧,
∴反比例函数值y2的取值范围为y2<0或y2>5;
(3)如图,过E作EM⊥y轴于点M,过F作FN⊥y轴于点N,过F作FP⊥EM于点P,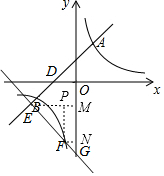
∵直线AB解析式为y=x+3,EF⊥AB,
∴∠EGM=∠EFP=∠MEG=45°,
∴EP=PF,FN=GN,
设E(t,t+3),F(s,$\frac{10}{s}$),
∴s-t=t+3-$\frac{10}{s}$,解得t=$\frac{s}{2}$+$\frac{5}{s}$-$\frac{3}{2}$,
∵EF=$\sqrt{2}$PE=$\sqrt{2}$(s-t),FG=$\sqrt{2}$(-s),
∴EF•FG=-2s(s-t)=-2s(s-$\frac{s}{2}$-$\frac{5}{s}$+$\frac{3}{2}$)=-s2-3s+10=-(s+$\frac{3}{2}$)2+$\frac{49}{4}$,
由直线AB与双曲线解析式可求得B(-5,-2),
∵点E在点B下方,
∴t<-5,即$\frac{s}{2}$+$\frac{5}{s}$-$\frac{3}{2}$<-5,解得s>-2,
∴当s=-$\frac{3}{2}$时,EF•FG有最大值$\frac{49}{4}$,
∴EF•FG的最大值为$\frac{49}{4}$.
点评 本题为反比例函数的综合应用,涉及待定系数法、等腰直角三角形的性质、勾股定理、方程思想及数形结合思想等知识.在(1)中注意待定系数法的应用,在(2)中注意数形结合思想的应用,在(3)中用E、F的坐标表示出EF•FG,得到一个二次函数,是解题的关键.本题考查知识点较多,综合性较强,难度较大.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案| A. | $\frac{1}{6}$ | B. | 6 | C. | -6 | D. | -$\frac{1}{6}$ |
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | a4÷a2=a2 | D. | (a2)4=a6 |
| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
| A. | 165,165 | B. | 165,170 | C. | 170,165 | D. | 170,170 |
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
| A. | 两点之间的距离 | B. | 点到直线的距离 | ||
| C. | 两条直线之间的距离 | D. | 空中飞行的距离 |
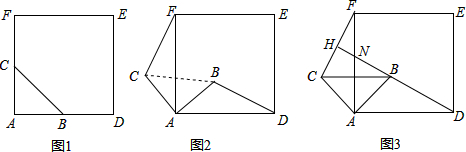
 如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )
如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )


