题目内容
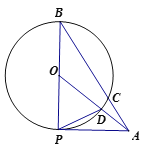
【题目】如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
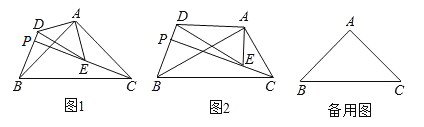
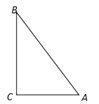
(1)问题提出:如图1,若AD=AE,AB=AC.
①∠ABD与∠ACE的数量关系为 ;②∠BPC的度数为 .
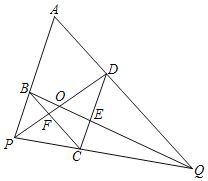
(2)猜想论证:如图2,若∠ADE=∠ABC=30°,则(1)中的结论是否成立?请说明理由.
(3)拓展延伸:在(1)的条件中,若AB=2,AD=1,若把△ADE绕点A旋转,当∠EAC=90°时,直接写出PB的长.
【答案】(1)①∠ABD=∠ACE,②90°;(2)(1)中结论成立,见解析;(3)PB的长为![]() 或
或![]() .
.
【解析】
(1)①依据等腰三角形的性质得到AB=AC,AD=AE,依据同角的余角相等得到∠DAB=∠CAE,然后依据“SAS”可证明△ADB≌△AEC,最后,依据全等三角形的性质可得到∠ABD=∠ACE;
②由三角形内角和定理可求∠BPC的度数;
(2)先判断出△ADB∽△AEC,即可得出结论;
(3)分为点E在AB上和点E在AB的延长线上两种情况画出图形,然后再证明△PEB∽△AEC,最后依据相似三角形的性质进行证明即可.
(1)①∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠DAB=∠CAE.∠ABC=∠ACB=45°,
∴△ADB≌△AEC(SAS),
∴∠ABD=∠ACE.
②∵∠BPC=180°﹣∠ABD﹣∠ABC﹣∠BCP=180°﹣45°﹣(∠BCP+∠ACE),∴∠BPC=90°.
故答案为:∠ABD=∠ACE,90°.
(2)(1)中结论成立,理由如下:
在Rt△ABC中,∠ABC=30°,
∴AB![]() AC.
AC.
在Rt△ADE中,∠ADE=30°,
∴AD![]() AE,
AE,
∴![]() .
.
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
∴△ADB∽△AEC,
∴∠ABD=∠ACE;
∵∠BPC=180°﹣∠ABD﹣∠ABC﹣∠BCP=180°﹣30°﹣(∠BCP+∠ACE),∴∠BPC=90°;
(3)①如图,当点E在AB上时,BE=AB﹣AE=1.

∵∠EAC=90°,
∴CE![]() .
.
同(1)可证△ADB≌△AEC,
∴∠DBA=∠ECA.
又∵∠PEB=∠AEC,
∴△PEB∽△AEC,
∴![]() ,
,
∴![]() ,
,
∴PB![]() ;
;
②如图,当点E在BA延长线上时,BE=AB+AE=3.

∵∠EAC=90°,
∴CE![]() .
.
同(1)可证△ADB≌△AEC,
∴∠DBA=∠ECA.
∵∠BEP=∠CEA,
∴△PEB∽△AEC,
∴![]() ,
,
∴![]() ,
,
∴PB![]() .
.
综上所述:PB的长为![]() 或
或![]() .
.

 53随堂测系列答案
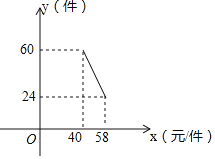
53随堂测系列答案【题目】某服装店以每件40元的价格购进一批衬衫,在试销过程中统计发现,每月的销售量y(件)与销售单价x(其中x为正整数,且50≤x≤75)(元)之间有下表关系:
销售单价x(元) | 50 | 55 | 60 | 65 | 70 | 75 |
每月销售量y(件) | 160 | 140 | 120 | 100 | 80 | 60 |
(1)若y与x之间的函数关系是下列函数关系之一,则y是x的______
A.正比例函数 B.一次函数 C.反比例函数 D.二次函数
(2)求y与x的函数关系式;
(3)如果不考虑其它费用,该店销售这种衬衫的月利润为1600元,这种衬衫的销售单价应定为多少元?
(4)如果每销售一件衬衫需要支出各种费用2元,设服装店每月销售这种衬衫获利为w元,销售单价为多少元时,服装店获利w最大,最大利润是多少?
【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
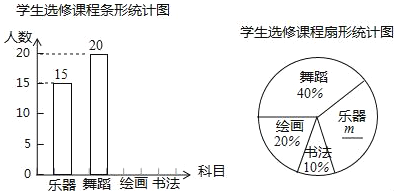
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)我市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?