题目内容
2.计算:(1)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
(2)(3+$\sqrt{5}$)2-(4+$\sqrt{7}$)(4-$\sqrt{7}$)
(3)($\sqrt{3}$+1)(3-$\sqrt{3}$)
(4)$\sqrt{3{a}^{2}}$÷(-3$\sqrt{\frac{a}{2}}$)×$\frac{1}{2}$$\sqrt{\frac{2a}{3}}$.
分析 (1)根据二次根式的乘除法则运算;
(2)利用完全平方公式和平方差公式计算;
(3)把后面括号内提$\sqrt{3}$,然后利用平方差公式计算;
(4)根据二次根式的乘除法则运算.
解答 解:(1)原式=$\sqrt{48÷3}$-$\sqrt{\frac{1}{2}×12}$+2$\sqrt{6}$
=4-$\sqrt{6}$+2$\sqrt{6}$
=4+$\sqrt{6}$;
(2)原式=9+6$\sqrt{5}$+5-(16-7)
=9+6$\sqrt{5}$+5-9
=6$\sqrt{5}$+5;
(3)原式=$\sqrt{3}$($\sqrt{3}$+1)($\sqrt{3}$-1)
=$\sqrt{3}$×(3-1)
=2$\sqrt{3}$;
(4)原式=-$\frac{1}{3}$×$\frac{1}{2}$×$\sqrt{3{a}^{2}•\frac{2}{a}•\frac{2a}{3}}$
=-$\frac{1}{6}$×2a
=-$\frac{1}{3}$a.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
13.同一平面内,两条不重合的直线的位置关系是( )
| A. | 平行或垂直 | B. | 平行或相交 | C. | 平行、相交或垂直 | D. | 相交 |
14.把方程3x+2y=4,化为用含字母y的代数式表示x的形式正确的是( )
| A. | y=-$\frac{3}{2}$x+2 | B. | y=$\frac{3}{2}$x-2 | C. | x=-$\frac{2y+4}{3}$ | D. | x=$\frac{4-2y}{3}$ |
11.计算$\frac{1}{x-1}$÷$\frac{x}{{x}^{2}-1}$的结果是( )
| A. | 1 | B. | x+1 | C. | $\frac{x+1}{x}$ | D. | $\frac{1}{x-1}$ |
12.已知方程组$\left\{\begin{array}{l}{5x+y=3}\\{ax+5y=4}\end{array}\right.$和$\left\{\begin{array}{l}{x-2y=5}\\{5x+by=1}\end{array}\right.$有相同的解,则a,b的值为( )
| A. | $\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-4}\\{b=-6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-6}\\{b=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=14}\\{b=2}\end{array}\right.$ |
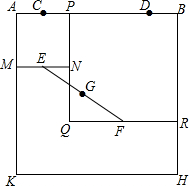 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )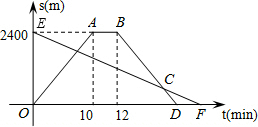 小华从家骑自行车出发,到相距2400米的银行办事,小华出发的同时,他哥哥以匀速的速度从银行沿同一条道路步行回家,小华在银行停留2分钟后沿原路以原速度返回,设他们出发后t分钟时,小华与家之间的距离为S1米,他哥与家之间的距离为S2米,如图中拆线OABD,线段EF分别是表示S1、S2与t之间函数关系的图象.
小华从家骑自行车出发,到相距2400米的银行办事,小华出发的同时,他哥哥以匀速的速度从银行沿同一条道路步行回家,小华在银行停留2分钟后沿原路以原速度返回,设他们出发后t分钟时,小华与家之间的距离为S1米,他哥与家之间的距离为S2米,如图中拆线OABD,线段EF分别是表示S1、S2与t之间函数关系的图象.